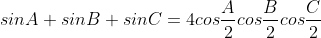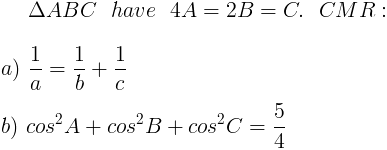tìm cực trị của biêủ thức
cos^3x.sin5x + sin^3x.cos5x
[tex]=\frac{1}{2}cos^2x(sin6x+sin4x)+\frac{1}{2}sin^2x(sin6x-sin4x)[/tex]
[tex]=\frac{1}{2}sin6x(cos^2x+sin^2x)+\frac{1}{2}sin4x(cos^2x-sin^2x)[/tex]
[tex] =\frac{1}{2}sin6x+\frac{1}{2}sin4xcos2x =\frac{1}{4}(sin6x+sin2x)+\frac{1}{2}sin6x=\frac{3}{4}sin6x+\frac{1}{4}sin2x[/tex]
[tex] \Rightarrow 2A=5sin2x-6sin^32x[/tex]
[tex]Dat-->sin2x=t..... |t| \le 1 [/tex]
[tex]2A=5t-6t^3[/tex]
[tex]Xet:: y=5t-6t^3 [/tex]
[tex]y'=5-18t^2[/tex]
[tex]y'=0 \Rightarrow \left[\begin{t=\sqrt{\frac{5}{18}} \\ t=-\sqrt{\frac{5}{18}}[/tex]
[tex]y(-1)=1[/tex]
[tex]y(1)=-1[/tex]
[tex]y(\sqrt{\frac{5}{18})}=5.\sqrt{\frac{5}{18}}-6.\sqrt{(\frac{5}{18}})^3=\sqrt{\frac{5}{18}} .\frac{10}{3}=\sqrt{\frac{250}{81}}=\frac{5\sqrt{10}}{9}[/tex]
[tex]y(-\sqrt{\frac{5}{18}})=-\sqrt{\frac{250}{81}}[/tex]
[tex]\Rightarrow A -min=\frac{-5\sqrt{10}}{18}\Leftrightarrow sin2x=-\sqrt{\frac{5}{18}}[/tex]
[tex]A-Max=\frac{5 \sqrt{10}}{18} \Leftrightarrow sin2x=\sqrt{\frac{5}{18}}[/tex]
Chẳng biết kết quả sao nữa



Khác với kết quả của duynhana1