[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
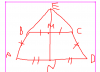
Cho hình thang cân ABCD (BC//AD). M, N là trung điểm BC, AD. Trên tia đối AB lấy P bất kì. PN cắt BD tại Q. CM: MN là phân giác góc PMQ.
Mình kiếm thấy có một bài y hệt vậy có lời giải chỉ cái mình thắc mắc là tại sao MN vuông góc AD thôi.
Link bài giải: https://diendan.hocmai.vn/threads/toan-9-chung-minh-phan-giac.374070
Ai giải thích hộ mình với, mình vẫn còn chưa hiểu khúc đó
Mình kiếm thấy có một bài y hệt vậy có lời giải chỉ cái mình thắc mắc là tại sao MN vuông góc AD thôi.
Link bài giải: https://diendan.hocmai.vn/threads/toan-9-chung-minh-phan-giac.374070
Ai giải thích hộ mình với, mình vẫn còn chưa hiểu khúc đó