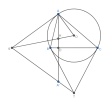
Gọi giao điểm của tiếp tuyến của [imath](O)[/imath] tại [imath]A[/imath] và trung trực của [imath]BC[/imath] là [imath]E[/imath], [imath]A_1[/imath] đối xứng với [imath]A[/imath] qua trung trực của [imath]BC[/imath]. [imath]AH,BO[/imath] cắt đường tròn tại [imath]H',I[/imath]. Khi đó dễ thấy [imath]A_1 \in (O)[/imath] và [imath]A_1,O,H'[/imath] thẳng hàng.
Theo định lý Thales, ta chỉ cần chứng minh [imath]\dfrac{OT}{OE}=\dfrac{HA'}{HA}[/imath]
Ta có: [imath]\dfrac{OA}{OE}=\cos \widehat{AOE}=\cos \widehat{ACA_1}=\sin \widehat{ACH'}=\dfrac{AH'}{2R}[/imath]
[imath]\dfrac{OB}{OT}=\cos \widehat{BOT}=\cos \widehat{A}=\sin \widehat{IAC}=\dfrac{IC}{2R} \Rightarrow \dfrac{OT}{OE}=\dfrac{IC}{AH'}[/imath]
Mặt khác, do [imath]A,A'[/imath] và [imath]H,H'[/imath] là [imath]2[/imath] cặp điểm đối xứng với nhau qua [imath]BC[/imath] nên [imath]AH'=A'H[/imath]
Từ đó ta cần chứng minh [imath]IC=AH[/imath]. Hiển nhiên đây là hệ quả của tính chất [imath]AHCI[/imath] là hình bình hành.
Bài toán được chứng minh hoàn tất.
Nếu còn thắc mắc chỗ nào bạn hãy trả lời dưới topic này để được hỗ trợ nhé ^^ Chúc bạn học tốt ^^
Ngoài ra, bạn tham khảo kiến thức tại đây nhé
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
