- 28 Tháng sáu 2020
- 287
- 380
- 81
- 18
- Hà Tĩnh
- Trường THCS Minh Lạc
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
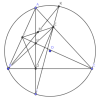
Cho [imath]\triangle A B C[/imath] có ba góc nhọn nội tiếp đường tròn [imath](O)[/imath]. Các đường cao [imath]A D, B E[/imath] và [imath]C F[/imath] của [imath]\triangle A B C[/imath] cắt
nhau tại [imath]H[/imath].
a) Chứng minh [imath]B C E F[/imath] và CDHE là các tứ giác nội tiếp.
b) Chứng minh [imath]E B[/imath] là tia phân giác của [imath]\widehat{F E D}[/imath] và [imath]\triangle B F E[/imath] đồng dạng với [imath]\triangle D H E[/imath].
c) Giao điểm của [imath]A D[/imath] vói đường tròn [imath](O)[/imath] là [imath]I(I \neq A)[/imath], IE cắt đường tròn [imath](O)[/imath] tại [imath]K(K \neq I)[/imath]. Gọi [imath]M[/imath] là trung điểm của đọn thẳng [imath]E F[/imath]. Chứng minh rằng ba điểm [imath]B, M, K[/imath] thẳng hàng.
Giúp e câu c với ạ
nhau tại [imath]H[/imath].
a) Chứng minh [imath]B C E F[/imath] và CDHE là các tứ giác nội tiếp.
b) Chứng minh [imath]E B[/imath] là tia phân giác của [imath]\widehat{F E D}[/imath] và [imath]\triangle B F E[/imath] đồng dạng với [imath]\triangle D H E[/imath].
c) Giao điểm của [imath]A D[/imath] vói đường tròn [imath](O)[/imath] là [imath]I(I \neq A)[/imath], IE cắt đường tròn [imath](O)[/imath] tại [imath]K(K \neq I)[/imath]. Gọi [imath]M[/imath] là trung điểm của đọn thẳng [imath]E F[/imath]. Chứng minh rằng ba điểm [imath]B, M, K[/imath] thẳng hàng.
Giúp e câu c với ạ
Attachments
Last edited by a moderator: