[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Giúp e câu c vs ạ
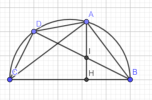
Cho nửa đường tròn đường kính [imath]B C[/imath], trên nửa đường tròn lấy điểm [imath]A[/imath] (khác B và [imath]\mathrm{C})[/imath]. Kẻ [imath]\mathrm{AH}[/imath] vuông góc với [imath]\mathrm{BC} (\mathrm{H}[/imath] thuộc [imath]B C[/imath] ). Trên cung [imath]A C[/imath] lấy điểm [imath]D[/imath] bất kì (khác [imath]A[/imath] và [imath]C[/imath] ), đường thẳng [imath]B D[/imath] cắt [imath]\mathrm{AH}[/imath] tại [imath]\mathrm{I}[/imath]. Chứng minh rằng:
1) IHCD là̀ tứ giác nội tiếp.
2) [imath]A B^{2}=B I.BD[/imath]
3) Tâm đường tròn ngoại tiếp tam giác AID luôn nằm trên một đường thẳng cố định khi D thay đổi trên cung [imath]A C[/imath].
Cho nửa đường tròn đường kính [imath]B C[/imath], trên nửa đường tròn lấy điểm [imath]A[/imath] (khác B và [imath]\mathrm{C})[/imath]. Kẻ [imath]\mathrm{AH}[/imath] vuông góc với [imath]\mathrm{BC} (\mathrm{H}[/imath] thuộc [imath]B C[/imath] ). Trên cung [imath]A C[/imath] lấy điểm [imath]D[/imath] bất kì (khác [imath]A[/imath] và [imath]C[/imath] ), đường thẳng [imath]B D[/imath] cắt [imath]\mathrm{AH}[/imath] tại [imath]\mathrm{I}[/imath]. Chứng minh rằng:
1) IHCD là̀ tứ giác nội tiếp.
2) [imath]A B^{2}=B I.BD[/imath]
3) Tâm đường tròn ngoại tiếp tam giác AID luôn nằm trên một đường thẳng cố định khi D thay đổi trên cung [imath]A C[/imath].
Attachments
Last edited by a moderator:
