View attachment 221543
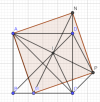
a) Xét [imath]\Delta ABM[/imath] và [imath]\Delta ADN[/imath] có
[imath]AB=AD, AM=AN, \widehat{BAM}= \widehat{DAN}[/imath] (cùng phụ với [imath]\widehat{MAD})[/imath]
[imath]\Rightarrow \Delta ABM\sim \Delta ADN[/imath]
[imath]\Rightarrow \widehat{ABM}= \widehat{ADN}=90^\circ[/imath]
Mà [imath]\widehat{ADC}=90^\circ[/imath]
Suy ra [imath]C,D,N[/imath] thẳng hàng
Gọi I là giao điểm của AP và MN
[imath]\Rightarrow I[/imath] là trung điểm của AP, MN
Xét [imath]\Delta CMN[/imath] vuông tại C, có I là trung điểm của MN\Rightarrow CI=\dfrac{MN}2$
Mà [imath]AI=\dfrac{MN}2[/imath] nên [imath]I[/imath] thuộc đường trung trực của AC
Mặt khác, [imath]BD[/imath] là đường trung trực của AC nên [imath]I\in BD[/imath]
Vậy BD cắt MN tại I là trung điểm của MN
b) Ta có: [imath]CI=\dfrac{AP}2\Rightarrow \Delta ACP[/imath] là tam giác vuông tại C
[imath]\Rightarrow \widehat{ACP}=90^\circ\Rightarrow \widehat{DCP}=45^\circ[/imath]
Vậy P thuộc tia gốc C hợp với [imath]DC[/imath] góc [imath]45^\circ[/imath] cố định
Có gì khúc mắc em hỏi lại nha
Ngoài ra, em xem thêm tại
Tổng hợp các bài toán hình học 8 thường gặp
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.