Cho tam giác ABC, BC:2x+y-4=0, đường tròn ngoại tiếp tam giác HBC: x^2+y^2-6x-6y+8=0 ( H là trực tâm tam giác ABC). Lập phương trình đường tròn ngoại tiếp tam giác ABC
hi1234567891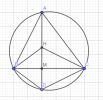
Gọi [imath]D; M[/imath] là giao điểm của [imath]AH[/imath] với đường tròn và với BC
ta có [imath]\widehat{BAD}=\widehat{BCH}[/imath] (cùng phụ với [imath]\widehat{ABC}[/imath])
mà [imath]\widehat{BAD}=\widehat{BCD}[/imath] (cùng chắn cung BD)
Suy ra [imath]\widehat{BCH}=\widehat{BCD}[/imath]
Xét [imath]\Delta HDC[/imath] có CM vừa là đường cao vừa là đường phân giác
[imath]\Rightarrow \Delta HCD[/imath] cân tại [imath]C[/imath]
suy ra [imath]H[/imath] là điểm đối xứng với [imath]D[/imath] qua [imath]BC[/imath]
[imath]\Rightarrow[/imath] tâm đường tròn ngoại tiếp của [imath]\Delta HBC[/imath] đối xứng với tâm đường tròn ngoại tiếp của [imath]\Delta DBC[/imath] qua BC
tới đây em làm tiếp nhé
e lấy đối xứng tâm ngoại tiếp của [imath]\Delta HBC[/imath] qua BC và viết pt đường tròn nhé ([imath]R_{HBC}=R_{DBC}[/imath])
Có gì khúc mắc em hỏi lại nhé
Ngoài ra em tham khảo thêm tại
Hệ thức lượng trong tam giác và diện tích tam giác
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
