- 24 Tháng mười 2018
- 1,616
- 1,346
- 216
- 25
- TP Hồ Chí Minh
- Đại học Sư phạm Kỹ thuật TP Hồ Chí Minh
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
1. Hệ thức lượng trong tam giác vuông
- cho tam giác ABC có [tex]\widehat{A}=90^o[/tex], ta có:
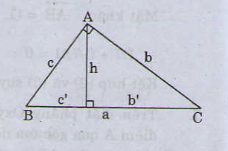
- [tex]b^2=ab'; c^2=ac'[/tex]
- pytago: [tex]a^2=b^2+c^2[/tex]
- [tex]a.h=b.c=2S[/tex]
- [tex]h^2=b'.c'[/tex]
[tex]\frac{1}{h^2}=\frac{1}{b^2}+\frac{1}{c^2}[/tex]
2. định lý hàm số cosin
Định lí: Trong một tam giác bất kì, bình phương một cạnh bằng tổng các bình phương của hai cạnh còn lại trừ đi hai lần tích của hai cạnh đó nhân với cosin của góc xen giữa chúng.
Ta có các hệ thức sau:
[tex]a^2=b^2+c^2-2bc.cos\widehat{A}[/tex]
[tex]b^2=a^2+c^2-2ac.cos\widehat{B}[/tex]
[tex]c^2=a^2+b^2-2ab.cos\widehat{C}[/tex]
từ đó, ta có thể suy ra công thức tính góc của 1 tam giác:
[tex]cos\widehat{A}=\frac{b^2+c^2-a^2}{2bc}[/tex]
mở rộng: tính độ dài trung tuyến của 1 tam giác.
cho tam giác ABC có 3 cạnh lần lượt là a, b, c và [tex]m_a, m_b, m_c[/tex] là 3 đường trung tuyến hạ từ các đỉnh tương ứng. ta có:
[tex]m_a^2=\frac{2.(b^2+c^2)-a^2}{4}[/tex]
[tex]m_b^2=\frac{2.(a^2+c^2)-b^2}{4}[/tex]
[tex]m_c^2=\frac{2.(a^2+b^2)-c^2}{4}[/tex]
3. định lý hàm số sin
Định lí: Trong tam giác ABC bất kỳ, tỉ số giữa một cạnh và sin của góc đối diện với cạnh đó bằng đường kính của đường tròn ngoại tiếp tam giác, nghĩa là:
[tex]\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=2R[/tex]
với R là bán kính đường tròn ngoại tiếp tam giác ABC.
4. diện tích tam giác
- cho tam giác ABC có [tex]\widehat{A}=90^o[/tex], ta có:

- [tex]b^2=ab'; c^2=ac'[/tex]
- pytago: [tex]a^2=b^2+c^2[/tex]
- [tex]a.h=b.c=2S[/tex]
- [tex]h^2=b'.c'[/tex]
[tex]\frac{1}{h^2}=\frac{1}{b^2}+\frac{1}{c^2}[/tex]
2. định lý hàm số cosin
Định lí: Trong một tam giác bất kì, bình phương một cạnh bằng tổng các bình phương của hai cạnh còn lại trừ đi hai lần tích của hai cạnh đó nhân với cosin của góc xen giữa chúng.
Ta có các hệ thức sau:
[tex]a^2=b^2+c^2-2bc.cos\widehat{A}[/tex]
[tex]b^2=a^2+c^2-2ac.cos\widehat{B}[/tex]
[tex]c^2=a^2+b^2-2ab.cos\widehat{C}[/tex]
từ đó, ta có thể suy ra công thức tính góc của 1 tam giác:
[tex]cos\widehat{A}=\frac{b^2+c^2-a^2}{2bc}[/tex]
mở rộng: tính độ dài trung tuyến của 1 tam giác.
cho tam giác ABC có 3 cạnh lần lượt là a, b, c và [tex]m_a, m_b, m_c[/tex] là 3 đường trung tuyến hạ từ các đỉnh tương ứng. ta có:
[tex]m_a^2=\frac{2.(b^2+c^2)-a^2}{4}[/tex]
[tex]m_b^2=\frac{2.(a^2+c^2)-b^2}{4}[/tex]
[tex]m_c^2=\frac{2.(a^2+b^2)-c^2}{4}[/tex]
3. định lý hàm số sin
Định lí: Trong tam giác ABC bất kỳ, tỉ số giữa một cạnh và sin của góc đối diện với cạnh đó bằng đường kính của đường tròn ngoại tiếp tam giác, nghĩa là:
[tex]\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=2R[/tex]
với R là bán kính đường tròn ngoại tiếp tam giác ABC.
4. diện tích tam giác
- [tex]S=\frac{1}{2}a.h_a=\frac{1}{2}b.h_b=\frac{1}{2}c.h_c[/tex]
- [tex]S=\frac{1}{2}absinC=\frac{1}{2}acsinB=\frac{1}{2}bcsinA[/tex]
- [tex]S=\frac{abc}{4R}[/tex], với R là bán kính đường tròn ngoại tiếp.
- [tex]S=p.r[/tex], với p là nửa chu vi tam giác, r là bán kính đường tròn nội tiếp tam giác.
- [tex]S=\sqrt{p(p-a)(p-b)(p-c)}[/tex], với p là nửa chu vi tam giác.

