[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
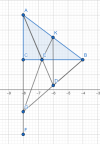
Cho △ABC vuông tại C có A^=60 độ và đường phân giác của BAC^ cắt BC tại E. Kẻ EK⊥AB tại K (K ∈ AB). Kẻ BD vuông góc với AE tại D (D ∈ AE). CM:
a, △ACE = △AKE
b, AE là đường trung trực của đoạn thẳng CK
c, KA=KB
d, KD // AC và EB>EC; AC + BD = AB
e, AC, KE, BD đồng quy
a, △ACE = △AKE
b, AE là đường trung trực của đoạn thẳng CK
c, KA=KB
d, KD // AC và EB>EC; AC + BD = AB
e, AC, KE, BD đồng quy