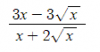ĐKXĐ: [tex]x>0[/tex].
Ta có:[tex]P=\frac{3x-3\sqrt{x}}{x+2\sqrt{x}}=\frac{3\sqrt{x}(\sqrt{x}-1)}{\sqrt{x}(\sqrt{x}+2)}=\frac{3(\sqrt{x}-1)}{\sqrt{x}+2}=\frac{3(\sqrt{x}+2)-9}{\sqrt{x}+2}=3-\frac{9}{\sqrt{x}+2}[/tex].
Để P nguyên thì [tex]\frac{9}{\sqrt{x}+2}[/tex] nguyên. (1)
Nếu
x không là số chính phương thì [tex]\sqrt{x}[/tex] vô tỉ nên [tex]\sqrt{x}+2[/tex] cũng vô tỉ.
Đặt [tex]\frac{9}{\sqrt{x}+2}=n[/tex] [tex](n\in \mathbb{Z})[/tex] thì [tex]\sqrt{x}+2=\frac{9}{n}[/tex] là số vô tỉ.
Mà [tex]\frac{9}{n}[/tex] là số hữu tỉ => Vô lí.
Vậy
x là số chính phương, khi đó [tex]\sqrt{x}+2[/tex] nguyên. (2)
Với ĐKXĐ thì [tex]\sqrt{x}+2\geq0+2=2[/tex]. (3)
Từ (1), (2), (3) suy ra [tex]\sqrt{x}+2[/tex] là ước không nhỏ hơn 2 của 9, tức là [tex]\sqrt{x}+2[/tex] bằng 3 hoặc 9.
Ta lập bảng sau:
| [tex]\sqrt{x}+2[/tex] | 3 | 9 |
| [tex]\sqrt{x}[/tex] | 1 | 7 |
| x | 1 | 49 |
[TBODY]
[/TBODY]
Vậy
x = 1 hoặc 49.
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.