BT1:
Bài đầu này chỉ để thử mức độ vận dụng của các bạn, chỉ khác ở phần thay số thôi
[imath]U_{Lr1}=I_1.Z_{Lr}\\ U_{Lr2}=I_2.Z_{Lr}\\ =>\frac{I_2}{I_1}=3[/imath]
chuẩn hóa[imath]I_1=1,I_1=3[/imath]
đây là hình chữ nhật=>[imath]\left\{\begin{matrix} U_{r_1}=U_{LC2}\\ U_{r_2}=U_{LC1} \end{matrix}\right. =>\left\{\begin{matrix} r=3(Z_L-\frac{Z_C}{3})\\ 3r=Z_C-Z_L \end{matrix}\right.[/imath]
tiếp tục chuẩn hóa r=1
=>[imath]Z_C=5,Z_L=2[/imath]
Ta có: [imath]\frac{U}{U_{Lr_1}}=\frac{\sqrt{r^2+(Z_L-Z_C)^2}}{\sqrt{r^2+Z_L^2}}\\
=>U=45\sqrt{2}(V)=>U_0=90(V)[/imath]
Vậy tại sao anh lại đưa lại bài này làm gì nhỉ, làm lại y xì thì có gì hay đâu, không nó có nguyên do cả đấy,ở lần trước anh đã nói bài này áp dụng giản đồ NAV chưa hẳn là tuyệt nhất (mặc dù nó đã khá gọn).
Trước đây trước khi các loại giản đồ siêu việt được ra mắt, các thầy cô và học sinh khi giải các bài tập này hầu như sử dụng một loại giản đồ mang tên "giản đồ kép".Tại sao lại là "kép", hiểu đơn giản là vì nó được ghép lại từ hại giản đồ véc tơ bình thường( trục I nằm ngang).Ko dài dòng nữa anh sẽ đi luôn vào loại giản đồ quốc dân thời xưa này:
III,Giản đồ kép
Cơ sở lý thuyết: Vì nó được xuất phát từ giản đồ vecto bình thường nên cũng không có gì đặc biệt, việc đơn giản là ghép hai giản đồ ở hai TH lên một hình vẽ và tính toán thôi.Nhưng chúng ta cũng cần có 1 vài điểm chú ý khi sử dụng loại giản đồ như sau:
-U là không đổi nên ta có thể biểu diễn AB bằng bán kính của một đường tròn có bán kính là U
-Trục I là nằm ngang
-Và mọi tính chất của giản đồ vecto thông thường(rL đi xiết lên,C hướng xuống,...)
Ta sẽ giải lấy luôn BT1 để làm ví dụ:
[imath]\vec{U}=\vec{U_{rl}}+\vec{U_C}[/imath]
Ở giản đồ này ta ko phải tách gì cả chỉ cần vẽ lần lượt như bình thường thôi
Khi lấy đường tròn tâm A bán kính là U thì B dù thế nào cũng nằm trên đường tròn ấy.
Ta lấy trục I nằm ngang,nhận xét vì ta chập 2 dòng điện làm một nên góc lệch giữa 2 I chính bằng góc lệch giữa 2 U trong hình vẽ này:
độ lệch pha giữa rL và I là: [imath]tan(\varphi)=\frac{Z_L}{r}[/imath]
do [imath]Z_L[/imath] và r không đổi trong 2 TH nên, góc [imath]\varphi [/imath] cũng là không đổi nên [imath]U_{rl_1},U_{rl_2}[/imath] sẽ nằm trên cùng 1 đường thẳng như hình vẽ( do cùng lệch I góc [imath]\varphi[/imath] ).
Tóm cái váy lại ta sẽ biểu diễn được hình như trên.Còn lại là phần tính toán bằng hình học:
[imath]\frac{I_2}{I_1}=\frac{U_{rl_2}}{U_{rl_1}}=3\\
\frac{Z_{C_2}}{Z_{C_1}}=\frac{C_1}{C_2}=\frac{1}{3}\\
=>U_{C_1}=U_{C_2}[/imath]
mà [imath]\vec{U_{C_1}}=\vec{U_{C_2}}[/imath]
=>[imath]M_1M_2B_2B_1[/imath] là 1 hình bình hành=>[imath]B_1B_2=M_1M_2=U_{rl_2}-U_{rl_1}=135-45=90(V)[/imath]
lại xét tam giác [imath]B_1AB_2[/imath] là 1 tam giác vuông tại A:
[imath]=>U^2+U^2=B_1B_2=>\sqrt{2}U=90=>U=45\sqrt{2}(V)\\
=>U_0=90(V)[/imath]
Nếu như ko phải giải thích dài dòng như ở trên thì phần tính toán là quá nhanh quá nguy hiểm phải không ạ.
Vậy tại sao người ta không áp dụng cách này, câu trả lời là do phạm vi áp dụng là quá hạn chế, chắc ai cũng nhận ra được điều đặc biệt ở bài này là hình bình hành, điều kiện để trở thành là 1 hình bình hành đó chính là [imath]U_C[/imath] phải ko đổi, nếu ko phải là hình bình hành thì giải theo cách này khá là phức tạp đấy, bạn thử làm câu 2 mà xem.
Vì nó quá đặc biệt nên người ta đã tổng quát thành một công thức như sau:
Nếu [imath]U_C[/imath] ko đổi , thì với giả sử độ lớn biến thiên của [imath]U_{rl}=\Delta U[/imath], góc lệch pha giữa 2 I là [imath]\varphi[/imath]:
=>[imath]2Usin(\frac{\varphi}{2})=\Delta U[/imath]=>[imath]U=\frac{\Delta U}{2sin(\frac{\varphi}{2})}[/imath]
CM khá là đơn giản:
[imath]B_1B_2=2B_1H[/imath] mà [imath]B_1H=U.sin(\frac{\varphi}{2})[/imath]
thay vào ta được công thức trên, các bạn nên ghi nhớ công thức nhanh kia nhé, phần áp dụng nhanh hơn khi gặp lại, trong một số bài tập nó có thể đóng vai trò làm một phương trình nữa<: .Nhưng hãy luôn nhớ đến điều kiện để áp dụng nó.
BT2:
Bài này áp dụng giản đồ kép là khá phức tạp, TH này giản đồ NAV tỏ ra ưu việt hơn tất cả:
Vẽ hình như cũ:
Cách giải là hoàn toàn tương tự :
[imath]U_{Lr1}=I_1.Z_{Lr}\\ U_{Lr2}=I_2.Z_{Lr}\\ =>\frac{I_2}{I_1}=\frac{7}{2}[/imath]
chuẩn hóa [imath]I_1=2,I_1=7[/imath]
[imath]\left\{\begin{matrix} U_{r_1}=U_{LC2}\\ U_{r_2}=U_{LC1} \end{matrix}\right. =>\left\{\begin{matrix} 2r=7(Z_L-\frac{Z_C}{3})\\ 7r=2(Z_C-Z_L) \end{matrix}\right.[/imath]
=>[imath]Z_L,Z_C[/imath] =>[imath]U_0=96,63(V)[/imath]
Tổng kết: qua chuyến du hành lần này mong rằng các bạn có thể nắm rõ hơn phần nào về hai loại giản đồ này về cội nguồn, cơ sở hay cách sử dụng thế nào cho hợp lý.Nếu thấy hay thì các bạn có thẻ để lại nút like để ủng hộ anh.Ngoài ra các bạn có thể tham khảo thêm chuyên đề bộ trợ nâng cao
giao thoa ánh sáng này và hẹn gặp các bạn lại lần sau.
Đây là bài tập thêm và chuẩn bị cho bài tiếp theo:
BT1:
Đặt điện áp [imath]u=U_0cos(\omega t)[/imath] vào hai đầu đoạn mạch gồm cuộn dây không thuần cảm mắc nối tiếp với tụ điện có điện dung [imath]C[/imath]thay đổi được.Khi [imath]C = C_0[/imath] thì cường độ dòng điện trong mạch sớm pha hơn [imath]u[/imath] là [imath]\varphi_1[/imath], [imath](0<\varphi < \frac{\pi}{2})[/imath] và điện áp hiệu dụng hai đầu cuộn dây là [imath]40V[/imath]. Khi [imath]C = 2C_0[/imath] thì cường độ dòng điện trong mạch trễ pha hơn [imath]u[/imath]là [imath]\varphi_2 = \frac{2\pi}{3}-\varphi_1[/imath] và điện áp hiệu dụng hai đầu cuộn dây là 120V. Tìm giá trị [imath]U_0[/imath]
BT2:
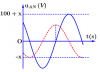
Mạch điện xoay chiều không phân nhánh gồm ba đoạn mạch AM, MN, NB ghép nối tiếp. AM chứa điện trở R, MN chứa cuộn dây thuần cảm có độ tự cảm L và NB chứa tụ điện có điện dung C thay đổi được. Khi [imath]C = C_1[/imath] và [imath]C = C_2[/imath] thì điện áp hiệu dụng hai đầu NB không đổi và bằng [imath]U_1[/imath] , phương trình trong hai trường hợp có đồ thị như hình bên. Điện áp hiệu dụng hai đầu mạch điện bằng bao nhiêu?
A. 50 V.
B. 100 V.
C. 150 V.
D. 75 V.
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
