[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
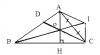
Cho tam giác ABC vuông tại A, đường cao AH, trung tuyến BM, phân giác CD cắt nhau tại một điểm. Chứng minh rằng:
a. BH/HC.CM/MA.AD/BD=1

b. BH=AC
Vẽ hình giúp em vs =(( Cần gấp trong tối nay ạ ((
((
a. BH/HC.CM/MA.AD/BD=1
b. BH=AC
Vẽ hình giúp em vs =(( Cần gấp trong tối nay ạ