[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
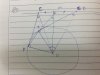
[TEX]\boxed{1}[/TEX]Cho tam giác ABC nhọn. Từ điểm A vẽ các tiếp tuyến AM,AN với đường tròn tâm O đường kính BC. Dựng đường cao AD của tam giác ABC. Gọi E là giao điểm của MN và AD. Chứng minh [TEX]AM^2=AE.AD[/TEX]
[TEX]\boxed{2}[/TEX]Cho hai đường tròn đồng tâm O với 2 bán kính R>r. Gọi A,M là hai điểm thuộc đường tròn (O,r). Qua M vẽ dây BC của đường tròn (O,R) sao cho BC vuông góc AM. Chứng minh [TEX]MA^2+MB^2+MC^2=2R^2+2r^2[/TEX]
[TEX]\boxed{3}[/TEX]Cho đường tròn đường kính AB và D là một điểm bất kì trên đường tròn. Tiếp tuyến tại A,D của (O) cắt nhau ở C. Gọi E là hình chiếu của D lên AB và F là giao điểm của BC và DE. Chứng minh [TEX]DF=EF[/TEX]
[TEX]\boxed{4}[/TEX]Từ một điểm M nằm ngoài (O) kẻ cát tuyến MAB và đường thẳng Mx vuông góc OM. Gọi C và D là giao điểm Mx với các tiếp tuyến tại A và B của (O). Chứng minh [TEX]MC=MD[/TEX]
[TEX]\boxed{5}[/TEX]Cho đường tròn (O) đường kính AB. Trên nửa đường tròn (O) lấy C,D sao cho A,B,C,D ko trùng nhau. Từ C vẽ CH vuông góc AB. Đường thẳng CH cắt (O) tại điểm thứ hai E. Từ A kẻ AK vuông góc CD. Đường thẳng AK cắt (O) tại điểm thứ hai F. Chứng minh [TEX]BE=DF[/TEX]
[TEX]\boxed{2}[/TEX]Cho hai đường tròn đồng tâm O với 2 bán kính R>r. Gọi A,M là hai điểm thuộc đường tròn (O,r). Qua M vẽ dây BC của đường tròn (O,R) sao cho BC vuông góc AM. Chứng minh [TEX]MA^2+MB^2+MC^2=2R^2+2r^2[/TEX]
[TEX]\boxed{3}[/TEX]Cho đường tròn đường kính AB và D là một điểm bất kì trên đường tròn. Tiếp tuyến tại A,D của (O) cắt nhau ở C. Gọi E là hình chiếu của D lên AB và F là giao điểm của BC và DE. Chứng minh [TEX]DF=EF[/TEX]
[TEX]\boxed{4}[/TEX]Từ một điểm M nằm ngoài (O) kẻ cát tuyến MAB và đường thẳng Mx vuông góc OM. Gọi C và D là giao điểm Mx với các tiếp tuyến tại A và B của (O). Chứng minh [TEX]MC=MD[/TEX]
[TEX]\boxed{5}[/TEX]Cho đường tròn (O) đường kính AB. Trên nửa đường tròn (O) lấy C,D sao cho A,B,C,D ko trùng nhau. Từ C vẽ CH vuông góc AB. Đường thẳng CH cắt (O) tại điểm thứ hai E. Từ A kẻ AK vuông góc CD. Đường thẳng AK cắt (O) tại điểm thứ hai F. Chứng minh [TEX]BE=DF[/TEX]
Last edited:
