[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
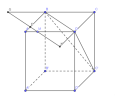
46. Cho hình hộp [imath]A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}[/imath]. Điểm [imath]M[/imath] là điểm thuộc cạnh [imath]A D[/imath] sao cho [imath]M D=3 M A \cdot[/imath] Mặt phẳng [imath](P)[/imath] qua [imath]M[/imath] và song song với mặt phẳng [imath]\left(B D C^{\prime}\right)[/imath], cắt [imath]C D[/imath] tại [imath]K[/imath]. Tỉ số [imath]\dfrac{K D}{K C}=\dfrac{m}{n}(m, n[/imath] là các số nguyên dương và nguyên tố cùng nhau). Tính giá trị biếu thức [imath]T=2 m^{2}+n^{2}[/imath].
[imath]A. T=67[/imath].
[imath]B. T=43[/imath].
[imath]C. T=17[/imath].
[imath]D. T=81[/imath].
ai giải chi tiết câu này giúp em ạ
[imath]A. T=67[/imath].
[imath]B. T=43[/imath].
[imath]C. T=17[/imath].
[imath]D. T=81[/imath].
ai giải chi tiết câu này giúp em ạ
Attachments
Last edited by a moderator: