 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Cho hàm số y=f(x) có đồ thị như hình vẽ:
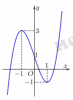
Có bao nhiêu giá trị nguyên của tham số m để phương trình $f(\cos x)=\sqrt[3]{m+2\sqrt[3]{2f(\cos x)+m}}$ có nghiệm :
A. 23
B. 24
C.20
D. 19
Bài này e ko biết làm, giúp e câu này với ạ ? E cảm ơn trước !

Có bao nhiêu giá trị nguyên của tham số m để phương trình $f(\cos x)=\sqrt[3]{m+2\sqrt[3]{2f(\cos x)+m}}$ có nghiệm :
A. 23
B. 24
C.20
D. 19
Bài này e ko biết làm, giúp e câu này với ạ ? E cảm ơn trước !
Attachments
Last edited by a moderator:

