- 14 Tháng năm 2017
- 3,974
- 7,627
- 744
- 23
- Phú Yên
- Trường THPT Lương Văn Chánh
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
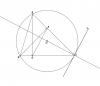
Cho [tex]\Delta[/tex] ABC có 3 góc nhọn nội tiếp đường tròn (O;R).
Hai đường cao AD và BE cắt nhau tại H (D [tex]\epsilon[/tex] BC;E [tex]\epsilon[/tex] AC; AB < AC).
Chứng minh OC vuông góc với DE.
Hai đường cao AD và BE cắt nhau tại H (D [tex]\epsilon[/tex] BC;E [tex]\epsilon[/tex] AC; AB < AC).
Chứng minh OC vuông góc với DE.