Vật lí Bài cơ học vật rắn khó (Lí 10 + 12)

[thuha2897]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

 

[Tùy Phong Khởi Vũ]

Xử cái này rồi ngủ.

Phân tích các lực tác dụng lên thanh như hình vẽ.


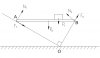
Áp dụng định luật II cho thanh ta được [TEX]\vec{F_1} + \vec{N_1}+\vec{F_2} + \vec{N_2}+\vec{P_1} + \vec{P_2} = 0[/TEX]

Chiếu lên phương ngang được [TEX]N_1.sina + F_1.cosa - N_2.cosa + F_2sina = 0[/TEX]

Chiếu lên phương thẳng đứng ta được:

[TEX]N_1.cosa - F_1.sina - P_2 - P_1 + N_2sina + F_2.cosa = 0[/TEX]

Lấy momen với B ta được pt cân bằng momen:

[TEX]N_1.L.cosa - F_1.L.sina - P_2.\frac{L}{2} - P_1.x = 0[/TEX] (L là chiều dài thanh)

Vì khoảng cách là cực tiểu, nên thanh ở trạng thái cân bằng giới hạn. Khi đó F1 và F2 phải đạt cực đại. Nghĩa là [TEX]F_1 = \mu.N_1, F_2 = N_2.\mu[/TEX]

Thay vào 3 pt trên ta được hệ 3 pt 3 ẩn là: N1 , N2 và x. Giải hệ là được.