Phần 2: BÀI TẬP SÁCH BÀI TẬP
3.1
Phần [imath]1[/imath]: [imath]C[/imath]
Giải thích: Chuyển động đều là chuyển động mà vận tốc có độ lớn không thay đổi theo thời gian, vì thế trong các khoảng thời gian bằng nhau vật đi được các quãng đường bằng nhau. Trên đoạn [imath]BC[/imath], vị trí hòn bi ở các khoảng thời gian bằng nhau cách nhau các khoảng bằng nhau nên hòn bi chuyển động đều trên đoạn đường này.
Phần [imath]2[/imath]: [imath]A[/imath]
Giải thích: Xét trên đoạn đường [imath]AB[/imath], trong các khoảng thời gian bằng nhau, vị trí hòn bi cách nhau với những khoảng cách tăng dần nên suy ra hòn bi chuyển động nhanh dần đều trên đoạn đường này. |  |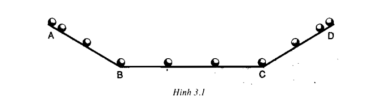
3.2 [imath]C[/imath]
Giải thích: Vận tốc trung bình của người đó trên hai quãng đường [imath]s1[/imath] và [imath]s2[/imath] là: [imath]v_{tb}=\dfrac{s_1+s_2}{t_1+t_2}[/imath]
3.3
Ta có: [imath]1\ km/h \ \approx 0,28 \ m/s[/imath] suy ra [imath]v_1=2 \ m/s = \dfrac{2}{0,28} \ km/h = \dfrac{50}{7} \ km/h[/imath]
- Thời gian người đó đi hết quãng đường đầu là: [imath]t_1=\dfrac{s_1}{v_1}=\dfrac{3}{\dfrac{50}{7}}=\dfrac{21}{50}h[/imath]
- Vận tốc trung bình của người đó trên cả quãng đường là: [imath]v_{tb}=\dfrac{s_1+s_2}{t_1+t_2}= \dfrac{3+1,95}{\dfrac{21}{50}+0,5} = \dfrac{495}{92} \ \approx 5,38 \ km/h[/imath]
3.4
[imath]a/[/imath] Chuyển động của vận động viên này trong cuộc đua là chuyển động không đều vì vận tốc của vận động viên thay đổi theo thời gian.
[imath]b/[/imath] Vận tốc trung bình của vận động viên: [imath]v_{tb} = \dfrac{s}{t}=\dfrac{100}{9,78} \approx 10,22 \ m/s = \dfrac{10,22}{0,28} \ km/h = 36,5 \ km/h[/imath] (vì [imath]1\ km/h \ \approx 0,28 \ m/s[/imath])
3.5
[imath]a/[/imath]
Vận tốc trung bình của vận động viên trong mỗi khoảng thời gian:
- [imath]20s[/imath] đầu tiên: [imath]v_1=\dfrac{s_1}{t_1}=\dfrac{140}{20}=7 \ m/s[/imath]
- Từ giây thứ [imath]20[/imath] đến giây thứ [imath]40[/imath]: [imath]v_2=\dfrac{s_2}{t_2}=\dfrac{340-140}{40-20}=10 \ m/s[/imath]
- Từ giây thứ [imath]40[/imath] đến giây thứ [imath]60[/imath]: [imath]v_3=\dfrac{s_3}{t_3}=\dfrac{428-340}{60-40}=4,4 \ m/s[/imath]
- Từ giây thứ [imath]60[/imath] đến giây thứ [imath]80[/imath]: [imath]v_4=\dfrac{s_4}{t_4}=\dfrac{516-428}{80-60}=4,4 \ m/s[/imath]
- Từ giây thứ [imath]80[/imath] đến giây thứ [imath]100[/imath]: [imath]v_5=\dfrac{s_5}{t_5}=\dfrac{604-516}{100-80}=4,4 \ m/s[/imath]
- Từ giây thứ [imath]100[/imath] đến giây thứ [imath]120[/imath]: [imath]v_6=\dfrac{s_6}{t_6}=\dfrac{692-604}{120-100}=4,4 \ m/s[/imath]
- Từ giây thứ [imath]120[/imath] đến giây thứ [imath]140[/imath]: [imath]v_7=\dfrac{s_7}{t_27}=\dfrac{780-692}{140-120}=4,4 \ m/s[/imath]
- Từ giây thứ [imath]140[/imath] đến giây thứ [imath]160[/imath]: [imath]v_8=\dfrac{s_8}{t_8}=\dfrac{880-780}{160-140}=5 \ m/s[/imath]
- Từ giây thứ [imath]160[/imath] đến giây thứ [imath]180[/imath]: [imath]v_9=\dfrac{s_9}{t_9}=\dfrac{1000-880}{180-160}=6 \ m/s[/imath] |
| Thời gian [imath](s)[/imath] | 0 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | | Quãng đường [imath](m)[/imath] | 0 | 140 | 340 | 428 | 516 | 604 | 692 | 780 | 880 | 1000 |
|
Nhận xét: Từ kết quả trên, ta thấy chuyển động của vận động viên là chuyển động không đều. Trong [imath]2[/imath] quãng đường đầu, vận động viên chạy nhanh dần (vận tốc tăng từ [imath]7 \ m/s[/imath] lên [imath]10 \ m/s[/imath]). Sau đó, vận động viên chuyển động đều trong [imath]5[/imath] quãng đường kế tiếp với vận tốc không đổi là [imath]4,4 \ m/s[/imath]. Ở [imath]2[/imath] quãng đường cuối, vận động viên chuyển động nhanh dần (vận tốc tăng từ [imath]5 \ m/s[/imath] lên [imath]6 \ m/s[/imath])
[imath]b/[/imath]
Vận tốc trung bình của vận động viên trong cả quãng đường:
[imath]v_{tb}=\dfrac{s_1+s_2+s_3+s_4+s_5+s_6+s_7+s_8+s_9}{t_1+t_2+t_3+t_4+t_5+t_6+t_7+t_8+t_9}[/imath]
[imath]=\dfrac{140+(340-140)+(428-340)+(516-428)+(604-516)+(692-604)+(780-692)+(880-780)+(1000-880)}{20+(40-20)+(60-40)+(80-60)+(100-80)+(120-100)+(140-120)+(160-140)+(180-160)}[/imath]
[imath]=\dfrac{76}{15} \ \approx 5m/s[/imath]
3.6
Đổi: [imath]t_1=2h15'=2,25h[/imath] ; [imath]t_2=24'=0,4h[/imath]
[imath]a/[/imath] Vận tốc trung bình trên mỗi quãng đường:
- Quãng đường [imath]AB[/imath]: [imath]v_1=\dfrac{s_1}{t_1}=\dfrac{45}{2,25}=20 \ km/h[/imath]
- Quãng đường [imath]BC[/imath]: [imath]v_2=\dfrac{s_2}{t_2}=\dfrac{30}{0,4}=75 \ km/h[/imath]
- Quãng đường [imath]CD[/imath]: [imath]v_3=\dfrac{s_3}{t_3}=\dfrac{10}{\dfrac{1}{4}}=40 \ km/h[/imath]
[imath]b/[/imath]
Vận tốc trung bình trên cả quãng đường:
[imath]v_{tb}=\dfrac{s_1+s_2+s_3}{t_1+t_2+t_3}=\dfrac{45+30+10}{2,25+0,4+\dfrac{1}{4}}=\dfrac{850}{29} \ \approx 29,31 \ km/h[/imath] |  |
3.7
Gọi quãng đường người đó di chuyển là [imath]S[/imath] ([imath]S>0,km[/imath])
Suy ra nửa quãng đường là [imath]\dfrac{S}{2}[/imath]
Thời gian đi nửa quãng đường đầu: [imath]t_1=\dfrac{\dfrac{S}{2}}{v_1}=\dfrac{S}{24}h[/imath]
Thời gian đi nửa quãng đường còn lại: [imath]t_2=\dfrac{\dfrac{S}{2}}{v_2}=\dfrac{S}{2v_2}h[/imath]
Vận tốc trung bình trên cả quãng đường: [imath]v_{tb}=\dfrac{\dfrac{S}{2}+\dfrac{S}{2}}{t_1+t_2}=\dfrac{S}{\dfrac{S}{24}+\dfrac{S}{2v_2}}=\dfrac{1}{\dfrac{1}{24}+\dfrac{1}{2v_2}}=8 \Rightarrow v_2=6 \ km/h[/imath]
3.8 [imath]D[/imath]
Giải thích: Chuyển động của vận động viên trượt tuyết từ dốc núi xuống, của vận động viên chạy [imath]100m[/imath] về đích và máy bay bay từ Hà Nội vào TP Hồ Chí Minh đều có vận tốc thay đổi theo thời gian
3.9 [imath]B[/imath]
Giải thích:
Gọi thời gian vật đi hết cả quãng đường là [imath]t[/imath] ([imath]t>0,s[/imath])
Quãng đường đi được trong [imath]\dfrac{1}{3}[/imath] thời gian đầu là: [imath]s_1=v_1.\dfrac{t}{3}=12.\dfrac{t}{3}=4t \ (m)[/imath]
Quãng đường đi được trong thời gian còn lại: [imath]s_2=v_2.(t-\dfrac{t}{3})=9.\dfrac{2t}{3}=6t \ (m)[/imath]
Vận tốc trung bình của vật trong suốt thời gian chuyển động là: [imath]v_{tb}=\dfrac{s_1+s_2}{t_1+t_2}=\dfrac{4t+6t}{\dfrac{t}{3} + \dfrac{2t}{3}}=10 \ (m/s)[/imath]
3.10
Gọi chiều dài mỗi đoạn đường là [imath]s[/imath] ([imath]s>0,m[/imath])
Thời gian xe chạy trên mỗi đoạn lần lượt là:
+, [imath]t_1=\dfrac{s}{v_1}=\dfrac{s}{12} s[/imath]
+, [imath]t_2=\dfrac{s}{v_}=\dfrac{s}{8} s[/imath]
+, [imath]t_1=\dfrac{s}{v_3}=\dfrac{s}{16} s[/imath]
Vận tốc trung bình trên cả chặng đường: [imath]v_{tb}=\dfrac{s+s+s}{t_1+t_2+t_3}=\dfrac{3s}{\dfrac{s}{12}+\dfrac{s}{8}+\dfrac{s}{16}}=\dfrac{144}{13} \ \approx 11 \ m/s[/imath]
3.11
Em học sinh thứ nhất chạy với vận tốc [imath]v_1[/imath] nhanh hơn em thứ hai chạy với vận tốc [imath]v_2[/imath] nên sau [imath]1s[/imath] khoảng cách giữa hai em là:[imath]s=v_1.1-v_2.2=0,8m[/imath]
Để hai em gặp nhau trong khoảng thời gian ngắn nhất thì em thứ nhất phải chạy nhanh hơn em thứ hai một vòng
Thời gian ngắn nhất để hai em gặp nhau là: [imath]t_{min}=\dfrac{C}{s}=\dfrac{400}{0,8}=500s= 8'20s[/imath]
3.12
[imath]a/[/imath]
Gọi [imath]t[/imath] là khoảng thời gian từ khi hai xe xuất phát tại Hà Nội ([imath]A[/imath]) và Đồ Sơn ([imath]B[/imath]) đến khi chúng gặp nhau tại vị trí [imath]C[/imath] trên hình.
Hai xe gặp nhau ta có:
[imath]AC+BC=AB[/imath]
[imath]\hArr v_1.t+v_2.t=t(v_1+v_2)=t.(45+15)=120[/imath]
[imath]\Rightarrow t = 2h[/imath]
Vậy sau [imath]2h[/imath] từ khi xuất phát thì hai xe gặp nhau
[imath]b/[/imath]
Nơi gặp cách Hà Nội một khoảng là:
[imath]AC=v_1.t=45.2=90 \ km[/imath] |  |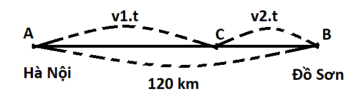
3.13
Đổi: [imath]20'=\dfrac{1}{3}h[/imath] ; [imath]30'=0,5h[/imath]; [imath]10'=\dfrac{1}{6}h[/imath]
Độ dài đoạn đường bằng: [imath]AC=v_1.t_1=45.\dfrac{1}{3}=15km[/imath]
Vận tốc trung bình khi leo dốc: [imath]v_2=\dfrac{v_1}{3}=\dfrac{45}{3}=15 \ km/h[/imath]
Vận tốc lúc xuống dốc: [imath]v_3=4.v_2=4.15=60 \ km/h[/imath]
Độ dài quãng đường lên dốc: [imath]CD=v_2.t_2=15.0,5=7,5 km[/imath]
Độ dài quãng đường xuống dốc: [imath]DB=v_3.t_3=60.\dfrac{1}{6}=10km[/imath]
Độ dài cả chặng đường [imath]AB[/imath]:
[imath]AB=AC+CD+DC=15+7,5+10=32,5 km[/imath] |  |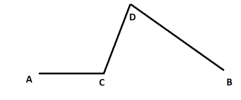
3.14
[imath]a/[/imath]
Gọi [imath]v_1,v_2[/imath] lần lượt là vận tốc cano và vận tốc dòng nước
- Khi xuôi dòng:
Vận tốc thực của cano là: [imath]v_{xuôi}=v_1+v_2[/imath]
Khoảng cách hai bến: [imath]MN = v_{xuôi}.t \hArr 120=(v_1+v_2).4 \Rightarrow v_1+v_2=30 \ km/h \ (1)[/imath]
- Khi ngược dòng:
Vận tốc thực của cano là: [imath]v_{ngược}=v_1-v_2[/imath]
Khoảng cách hai bến: [imath]MN=v_{ngược}.(t+2) \hArr 120=(v_1-v_2).(4+2) \Rightarrow v_1-v_2 = 20 \ km/h \ (2)[/imath]
Giải hệ [imath]2[/imath] phương trình [imath](1)[/imath] và [imath](2)[/imath] suy ra [imath]v_1=25 \ km/h, \ v_2=5 \ km/h[/imath]
Vậy vận tốc cano là [imath]25 \ km/h[/imath], vận tốc dòng nước là [imath]5 \ km/h[/imath]
[imath]b/[/imath]
Khi cano tắt máy thì vận tốc cano bằng vận tốc dòng nước, hay [imath]v_1=v_2=5 \ km/h[/imath]
Thời gian cano tắt máy đi từ [imath]M[/imath] đến [imath]N[/imath] là: [imath]t' = \dfrac{MN}{v_1}=\dfrac{120}{5}=24h[/imath]
3.15
[imath]a/[/imath]
Thời gian toa thứ nhất qua trước mặt người quan sát: [imath]t=9-0,5.5=6,5s[/imath]
[imath]b/[/imath]
Thời gian đoàn tàu qua trước mặt người quan sát: [imath]t' = 9+8,5+8+7,5+6,5=46,5s[/imath]
Chiều dài mỗi toa là [imath]10m[/imath] vậy chiều dài cả đoàn tàu là: [imath]L=10.6=60m[/imath]
Vận tốc trung bình của đoàn tàu lúc vào ga: [imath]v_{tb}=\dfrac{L}{t'}=\dfrac{60}{46,5} \approx 1,29s[/imath]
3.16
[imath]a/[/imath]
Vì ô tô và đoàn tàu chuyển động ngược chiều nhau nên vận tốc ô tô so với đoàn tàu: [imath]v=v_1+v_2=54+36=90 \ km/h = 90.0,28 \ m/s = 25,2 \ m/s[/imath] (vì [imath]1 \ km/h \approx 0,28 \ m/s[/imath])
Chiều dài đoàn tàu: [imath]L=v.t=25,2.3=75,6m[/imath]
[imath]b/[/imath]
Khi ô tô chuyển động đuổi theo đoàn tàu (tức là chuyển động cùng chiều đoàn tàu), vận tốc ô tô so với đoàn tàu là: [imath]v'= v_1 - v_2 = 54 - 36=18 \ km/h = 18.0,28 \ m/s = 5,04 \ m/s[/imath] (vì [imath]1 \ km/h \approx 0,28 \ m/s[/imath])
Thời gian ô tô vượt hết chiều dài đoàn tàu: [imath]t' = \dfrac{L}{v'}=\dfrac{75,6}{5,04}=15s[/imath]
3.17 [imath]C[/imath]
Giải thích:
Chuyển động "lắc lư" của con lắc đồng hồ là chuyển động không đều:
- Từ vị trí [imath]1[/imath] đến vị trí [imath]2[/imath]: chuyển động nhanh dần vì chuyển động từ cao xuống thấp
- Từ vị trí [imath]2[/imath] đến vị trí [imath]3[/imath]: chuyển động chậm dần vì chuyển động từ thấp lên cao |  |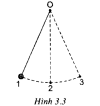
3.18 [imath]B[/imath]
Giải thích:
Đổi: [imath]15 \ m/s = \dfrac{15}{0,28} \ km/h \approx 54 \ km/h[/imath] (vì [imath]1 \ km/h \approx 0,28 \ m/s[/imath])
Thời gian đi của xe mô tô trên mỗi quãng đường:
+, Đoạn đường thứ nhất: [imath]t_1 = \dfrac{s_1}{v_1}=\dfrac{2}{36}=\dfrac{1}{18}h[/imath]
+, Đoạn đường thứ hai: [imath]t_2 = \dfrac{s_2}{v_2}=\dfrac{9}{}=\dfrac{1}{6}h[/imath]
+, Đoạn đường thứ ba: [imath]t_3 = \dfrac{s_3}{v_3}=\dfrac{5}{45}=\dfrac{1}{9}h[/imath]
Vận tốc trung bình trên cả quãng đường của mô tô: [imath]v_{tb}=\dfrac{s_1+s_2+s_3}{t_1+t_2+t_3}=\dfrac{2+9+5}{\dfrac{1}{18}+\dfrac{1}{6}+\dfrac{1}{9}}=48 \ km/h[/imath]
3.19 [imath]B[/imath]
Giải thích:
Người soát vé đi về phía đầu tàu suy ra người soát vé chuyển động cùng chiều với đoàn tàu
Vận tốc người soát vé so với đất:
[imath]v_{người/đất}=v_{người/tàu}+v_{tàu/đất}=3+36=39 \ km/h[/imath]
-------
Xem thêm:
Bài 2: Vận tốc |
Bài 4: Biểu diễn lực
Hocmai Forum 
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
