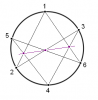
Giả sử ta có các điểm như hình vẽ. Ta sẽ chứng minh $K, J, L$ thẳng hàng. Áp dụng định lý Menelaus cho tam giác $GHI$ với các bộ điểm thẳng hàng: $D,K,C$; $A,J,B$ và $E,L,F$
$$\begin{array}{cc} \textbf{Bộ điểm} & \textbf{Định lý Menelaus} \\
D,K,C & \dfrac{HK}{GK} \cdot \dfrac{GC}{IC} \cdot \dfrac{ID}{HD} = 1 \\
A,J,B & \dfrac{HA}{GA} \cdot \dfrac{GB}{IB} \cdot \dfrac{IJ}{HJ} = 1 \\
E,L,F & \dfrac{HF}{GF} \cdot \dfrac{GL}{IL} \cdot \dfrac{IE}{HE} = 1 \\
\end{array}$$
Nhân các đẳng thức vế theo vế rồi biến đổi ta được
$$\dfrac{HK}{GK} \cdot \dfrac{GL}{IL} \cdot \dfrac{IJ}{HJ} \cdot (\dfrac{ID\cdot IE}{IB \cdot IC}) \cdot (\dfrac{HF \cdot HA}{HD \cdot HE}) \cdot (\dfrac{GC \cdot GB}{GA \cdot GF}) = 1$$
Ba biểu thức trong ngoặc đều bằng $1$ (phương tích của các điểm bên trong đường tròn), khi đó ta có
$$\dfrac{HK}{GK} \cdot \dfrac{GL}{IL} \cdot \dfrac{IJ}{HJ} = 1,$$
và theo định lý Menelaus đảo thì ba điểm $K, L, J$ cùng nằm trên một đường thằng, nói cách khác, $K, L, J$ thẳng hàng. Hoàn tất chứng minh định lý Pascal
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
