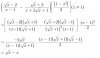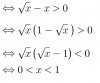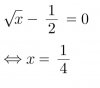a,Rút gọn
b,Tìm x để biểu thức >0
c,Tìm GTLN
a) ĐK: $x \geqslant 0$ và $x\ne 1$
$\left[ \dfrac{\sqrt{x}-2}{x-1} - \dfrac{\sqrt{x}+2}{x+2\sqrt{x}+1} \right] \cdot \dfrac{(1-x)^2}2 \\
= \dfrac{(\sqrt{x}-2)(\sqrt{x}+1) - (\sqrt{x}+2)(\sqrt{x}-1)}{(\sqrt{x}+1)^2(\sqrt{x}-1)} \cdot \dfrac{(x-1)^2}2 \\
= \dfrac{-2\sqrt{x}}{(\sqrt{x}+1)^2(\sqrt{x}-1)} \cdot \dfrac{(\sqrt{x}+1)^2(\sqrt{x}-1)^2}2 \\
= -\sqrt{x}(\sqrt{x}-1)$
b) Biểu thức $> 0 \iff -\sqrt{x}(\sqrt{x}-1) > 0 \iff \sqrt{x}(\sqrt{x}-1) < 0 \iff 0 < \sqrt{x} < 1 \iff 0 < x < 1$
Vậy ...
c) Ta có $-\sqrt{x}(\sqrt{x}-1) = -x + \sqrt{x} = -x + \sqrt{x} - \dfrac14 + \dfrac14 = -\left( \sqrt{x} - \dfrac12 \right)^2 + \dfrac14 \leqslant \dfrac14$
Vậy giá trị lớn nhất của biểu thức là $\dfrac14$ tại $\sqrt{x} = \dfrac12 \iff x= \dfrac14$ (N)
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.