- 27 Tháng mười 2018
- 3,742
- 3,706
- 561
- Hà Nội
- Trường Đại học Bách Khoa Hà Nội
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Bài toán về mặt cầu ngoại tiếp khối chóp, đa diện, có thể nhiều bạn đã biết nhưng bài toán về mặt cầu nội tiếp thì ít người biết đến. Về cơ bản việc tìm tâm mặt cầu nội tiếp khó hơn rất nhiều. Nên việc xác định bán kính mặt cầu nội tiếp 1 khối chóp chúng ta sẽ xác định qua 1 công thức được chứng minh:
Xét trường hợp riêng là 1 khối chóp tam giác(với các đa diện tứ giác cách chứng minh là tương tự...)
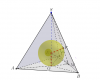
Ta có mặt cầu (E) nội tiếp khối chóp S.ABC. Ta kẻ các đường bán kính xuống các mặt bên và đáy, minh họa 2 đường bán kính EO và EF xuống mặt bên (SBC) và (ABC) như hình
Ta có từ tâm E ta có thể chia khối chóp S.ABC thành 4 khối chóp: E.SAC ; E.SBC ; E. SAB ; E.ABC
Vậy [TEX]V_{S.ABC}=V_{E.SAC}+V_{E.SBC}+V_{E.SAB}+V_{E.ABC}[/TEX]
Mà [TEX]V_{E.SBC} = 1/3 . EF. S_{SBC}=1/3. r. S_{SBC}[/TEX]
Với r là bán kính mặt cầu nội tiếp. Tương tự với 3 phần chóp còn lại. Vậy đặt nhân tử chung ta có:
[TEX]V_{S.ABC}=1/3. r. (S_{SAB}+S_{SBC}+S_{SAC}+S_{ABC})= 1/3. r. S_{tp}[/TEX]
[TEX]=>r=3V_{S.ABC} / S_{tp}[/TEX]
Với [TEX]S_{tp}[/TEX] là diện tích toàn phần của khối chóp, tức ta tính tổng diện tích tất cả các mặt bên và đáy.
Một cách tổng quát ta suy ra công thức tính bán kính r như sau:
[tex]r=\frac{3.V_{chop}}{S_{tp}}[/tex]
Các bạn chỉ cần nhớ công thức kết luận cuối cùng này. Nếu như gặp bài toán hình chóp có mặt cầu nội tiếp thì đó sẽ là chóp có các cạnh bên bằng nhau, các cạnh đáy bằng nhau. Như vậy việc tính S toàn phần sẽ rất nhanh.
*Tính bán kính mặt cầu nội tiếp của hình chóp đều [TEX]S_{ABCD}[/TEX] có tất cả các cạnh bằng 1.
Giải:
4 mặt bên bằng nhau nên diện tích 4 mặt bên là:
[tex]4.S_{SAB}=4.\frac{1}{2}.1.1.sin60=\sqrt{3}[/tex]
Vậy [TEX]S_{tp} = \sqrt{3} +1 [/TEX]
Ta có chiều cao SH=[tex]\frac{1}{\sqrt{2}}=>V_{SABCD}=\frac{1}{3}.\frac{1}{\sqrt{2}}.1=\frac{\sqrt{2}}{6}[/tex]
Vậy bán kính cần tìm là:
[tex]r=\frac{3.V_{SABCD}}{S_{tp}}=\frac{\frac{\sqrt{2}}{2}}{\sqrt{3}+1}[/tex] =[tex]\frac{\sqrt{2}}{2(\sqrt{3}+1)}[/tex]
Xét trường hợp riêng là 1 khối chóp tam giác(với các đa diện tứ giác cách chứng minh là tương tự...)
Ta có mặt cầu (E) nội tiếp khối chóp S.ABC. Ta kẻ các đường bán kính xuống các mặt bên và đáy, minh họa 2 đường bán kính EO và EF xuống mặt bên (SBC) và (ABC) như hình
Ta có từ tâm E ta có thể chia khối chóp S.ABC thành 4 khối chóp: E.SAC ; E.SBC ; E. SAB ; E.ABC
Vậy [TEX]V_{S.ABC}=V_{E.SAC}+V_{E.SBC}+V_{E.SAB}+V_{E.ABC}[/TEX]
Mà [TEX]V_{E.SBC} = 1/3 . EF. S_{SBC}=1/3. r. S_{SBC}[/TEX]
Với r là bán kính mặt cầu nội tiếp. Tương tự với 3 phần chóp còn lại. Vậy đặt nhân tử chung ta có:
[TEX]V_{S.ABC}=1/3. r. (S_{SAB}+S_{SBC}+S_{SAC}+S_{ABC})= 1/3. r. S_{tp}[/TEX]
[TEX]=>r=3V_{S.ABC} / S_{tp}[/TEX]
Với [TEX]S_{tp}[/TEX] là diện tích toàn phần của khối chóp, tức ta tính tổng diện tích tất cả các mặt bên và đáy.
Một cách tổng quát ta suy ra công thức tính bán kính r như sau:
[tex]r=\frac{3.V_{chop}}{S_{tp}}[/tex]
Các bạn chỉ cần nhớ công thức kết luận cuối cùng này. Nếu như gặp bài toán hình chóp có mặt cầu nội tiếp thì đó sẽ là chóp có các cạnh bên bằng nhau, các cạnh đáy bằng nhau. Như vậy việc tính S toàn phần sẽ rất nhanh.
*Tính bán kính mặt cầu nội tiếp của hình chóp đều [TEX]S_{ABCD}[/TEX] có tất cả các cạnh bằng 1.
Giải:
4 mặt bên bằng nhau nên diện tích 4 mặt bên là:
[tex]4.S_{SAB}=4.\frac{1}{2}.1.1.sin60=\sqrt{3}[/tex]
Vậy [TEX]S_{tp} = \sqrt{3} +1 [/TEX]
Ta có chiều cao SH=[tex]\frac{1}{\sqrt{2}}=>V_{SABCD}=\frac{1}{3}.\frac{1}{\sqrt{2}}.1=\frac{\sqrt{2}}{6}[/tex]
Vậy bán kính cần tìm là:
[tex]r=\frac{3.V_{SABCD}}{S_{tp}}=\frac{\frac{\sqrt{2}}{2}}{\sqrt{3}+1}[/tex] =[tex]\frac{\sqrt{2}}{2(\sqrt{3}+1)}[/tex]
