a) [imath]y=\log_2|x|[/imath]
Tập xác định: [imath]D=(-\infty,0) \cup (0,\infty)[/imath]
Vì [imath]|x|=x[/imath] khi [imath]x>0[/imath] và [imath]|x|=-x[/imath] khi [imath]x<0[/imath] nên ta có thể viết lại hàm số thành:
[math]y=\begin{cases} \log_2x, x>0 \\ \log_2(-x), x<0\end{cases}[/math]Do vậy ta chỉ cần vẽ đồ thị hàm [imath]y=log_2x[/imath] và [imath]y=log_2(-x)[/imath] trên 1 cùng hệ trục [imath]Oxy[/imath] là sẽ được đồ thị hàm [imath]y=\log_2|x|[/imath]
Đồ thị hàm [imath]y=\log_2(x)[/imath] là đồ thị cơ bản (giống như đồ thị của hàm số bậc 2 [imath]y=x^2[/imath]) nên ta phải nhớ để phát họa.
Còn đồ thị [imath]y=\log_2(-x)[/imath] là ta lấy đối xứng qua trục tung đồ thị của hàm [imath]y=\log_2x[/imath]
Nếu muốn vẽ chính xác thì mình nghĩ cần thêm các điểm tọa độ.
Hình tha
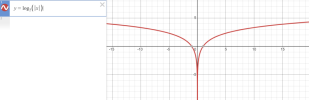
m khảo:
b) [imath]y=|\log_3x|[/imath]
Tập xác định: [imath]D=(0,\infty)[/imath]
Ta có:
[math]\log_3x \geq 0 \Leftrightarrow \log_3x \geq \log_31 \Leftrightarrow x \geq 1[/math][math]\log_3x<0 \Leftrightarrow \log_3x<\log_31 \Leftrightarrow 0<x<1[/math]Vậy ta có thể viết lại hàm số thành:
[math]y=\begin{cases} \log_3x , x\geq 1 \\ -\log_3x, 0<x<1 \end{cases}[/math]Tương tự ta sẽ vẽ đồ thị hàm [imath]y=\log_3x[/imath] khi [imath]x\geq 1[/imath] và hàm [imath]y=-\log_3x[/imath] khi [imath]0<x<1[/imath] để có được đồ thị của [imath]y=|\log_3x|[/imath].
Chú ý: Đồ thị của hàm [imath]y=-\log_3x[/imath] chính là đồ thị của hàm [imath]=\log_3x[/imath] lấy đối xứng qua trục [imath]Ox[/imath].
Hình tham khảo
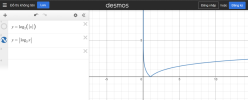
c) [imath]y=\log_{\dfrac{1}{3}}(x-2)=\log_{3^{-1}}(x-2)=\dfrac{1}{-1}\log_3(x-2)=-\log_3(x-2)[/imath]
Tập xác định: [imath]D=(2,\infty)[/imath]
Ta chỉ cần tịnh tiến đồ thị hàm [imath]y=\log_3x[/imath] sang phải 2 đơn vị vì có [imath]x-2[/imath] sau đó lấy đối xứng qua trục [imath]Ox[/imath] vì có dấu trừ trước hàm.
Hình tham khảo ở desmos nhé.
Nói chung để làm được bạn cần hiểu cách tịnh tiến đồ thị thì bạn sẽ hiểu tại sau mình làm như trên !
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
