- 12 Tháng mười một 2020
- 76
- 43
- 26
- 20
- Hà Nội
- Trung học phổ thông Quang Trung
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
F(x) =|x+2|+3|x-1|-6|x|-x
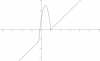
F(x)=|2x^2-3x-2|-2x^2+4x
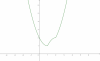
F(x) =x+|x^2-3x+2|
( Vẽ đồ thị hàm số trên và giải thích chi tiết do đâu mà vẽ như vậy )
F(x)=|2x^2-3x-2|-2x^2+4x
F(x) =x+|x^2-3x+2|
( Vẽ đồ thị hàm số trên và giải thích chi tiết do đâu mà vẽ như vậy )