- 24 Tháng mười 2018
- 1,616
- 1,346
- 216
- 25
- TP Hồ Chí Minh
- Đại học Sư phạm Kỹ thuật TP Hồ Chí Minh
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
1. từ định nghĩa tích phân
- F(x) là một nguyên hàm của f(x) trên đoạn [a;b] [tex]=>F(b)-F(a)=\int_{a}^{b}f(x)dx[/tex]
- f(x) là một nguyên hàm của f'(x) trên đoạn [a;b] [tex]=>f(b)-f(a)=\int_{a}^{b}f'(x)dx[/tex]
Bài toán tìm GTLN, GTNN của hàm số y=f(x) trên đoạn [a;b]:
- tính f'(x).
- giải phương trình f'(x)=0, nhận các nghiệm [tex]x_0\in [a;b][/tex]
- [tex]minf(x)=min\left \{ f(a),f(b),f(x_0) \right \}[/tex]
- [tex]maxf(x)=max\left \{ f(a),f(b),f(x_0) \right \}[/tex]
một số bài toán yêu cầu phải so sánh các giá trị [tex]f(a),f(b),f(x_0)[/tex] với nhau. khi đó ta cần phải sử dụng định nghĩa tích phân để so sánh:
- nếu [tex]\int_{x_1}^{x_2}f'(x)dx\geq 0=>f(x_2)\geq f_(x_1)[/tex]
- nếu [tex]\int_{x_1}^{x_2}f'(x)dx\leq 0=>f(x_2)\leq f_(x_1)[/tex]
ví dụ 1: cho hàm số y=f(x) có đồ thị f'(x) như hình vẽ:
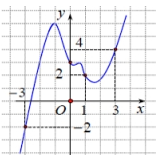
đặt [tex]g(x)=2f(x)-(x+1)^2[/tex]. so sánh các giá trị g(-3), g(1), g(3).
giải:
ta có: [tex]g'(x)=2.f'(x)-2.(x+1)[/tex]
<=> [tex]\frac{g'(x)}{2}=f'(x)-(x+1)[/tex]
xét: [tex]g'(x)=0<=>f'(x)=x+1[/tex]
xét tương giao giữa f'(x) và đường thẳng y=x+1, ta tìm được các giao điểm là:
[tex](-3;-2),(1;2), (3;4)[/tex] .
nên: [tex]g'(x)=0<=>x=\left \{ -3;1;3 \right \}[/tex].
đồ thị f'(x) và đường thẳng y=x+1 cắt nhau tạo thành 2 miền kín, miền lớn bên trái và nhỏ bên phải.
diện tích miền bên trái:
[tex]S_1=\int_{-3}^{1}|f'(x)-(x+1)|dx=\int_{-3}^{1}(f'(x)-(x+1))dx> 0<=>\frac{g(1)}{2}>\frac{g(-3)}{2}<=>g(1)>g(-3)[/tex]
diện tích miền bên phải:
[tex]S_2=\int_{1}^{3}|f'(x)-(x+1)|dx=\int_{1}^{3}-(f'(x)-(x+1))dx> 0<=>\frac{g(1)}{2}>\frac{g(3)}{2}<=>g(1)>g(3)[/tex]
mà [tex]S_1>S_2=>g(3)>g(-3)[/tex].
vậy, g(1)>g(3)>g(-3).
ví dụ 2: cho hàm số y=f(x) có đồ thị f'(x) như hình vẽ,cắt trục hoành lần lượt tại a, b, c với a<b<c, biết f(c)<0. tìm số nghiệm của phương trình f(x)=0.
giải:
xét miền kín phía dưới trục Ox: [tex]S_1=\int_{a}^{b}\left |f'(x) \right |dx=\int_{a}^{b}-f'(x)dx> 0<=>f(a)>f(b)[/tex]
xét miền kín phía trên trục Ox: [tex]S_1=\int_{b}^{c}\left |f'(x) \right |dx=\int_{b}^{c}f'(x)dx> 0<=>f(c)>f(b)[/tex]
do diện tích miền trên lớn hơn diện tích miền dưới nên f(c)>f(a).
mà f(c)<0 nên suy ra f(a), f(b)<0.
lập bảng biến thiên, ta thấy phương trình f(x)=0 vô nghiệm.
- F(x) là một nguyên hàm của f(x) trên đoạn [a;b] [tex]=>F(b)-F(a)=\int_{a}^{b}f(x)dx[/tex]
- f(x) là một nguyên hàm của f'(x) trên đoạn [a;b] [tex]=>f(b)-f(a)=\int_{a}^{b}f'(x)dx[/tex]
Bài toán tìm GTLN, GTNN của hàm số y=f(x) trên đoạn [a;b]:
- tính f'(x).
- giải phương trình f'(x)=0, nhận các nghiệm [tex]x_0\in [a;b][/tex]
- [tex]minf(x)=min\left \{ f(a),f(b),f(x_0) \right \}[/tex]
- [tex]maxf(x)=max\left \{ f(a),f(b),f(x_0) \right \}[/tex]
một số bài toán yêu cầu phải so sánh các giá trị [tex]f(a),f(b),f(x_0)[/tex] với nhau. khi đó ta cần phải sử dụng định nghĩa tích phân để so sánh:
- nếu [tex]\int_{x_1}^{x_2}f'(x)dx\geq 0=>f(x_2)\geq f_(x_1)[/tex]
- nếu [tex]\int_{x_1}^{x_2}f'(x)dx\leq 0=>f(x_2)\leq f_(x_1)[/tex]
ví dụ 1: cho hàm số y=f(x) có đồ thị f'(x) như hình vẽ:
đặt [tex]g(x)=2f(x)-(x+1)^2[/tex]. so sánh các giá trị g(-3), g(1), g(3).
giải:
ta có: [tex]g'(x)=2.f'(x)-2.(x+1)[/tex]
<=> [tex]\frac{g'(x)}{2}=f'(x)-(x+1)[/tex]
xét: [tex]g'(x)=0<=>f'(x)=x+1[/tex]
xét tương giao giữa f'(x) và đường thẳng y=x+1, ta tìm được các giao điểm là:
[tex](-3;-2),(1;2), (3;4)[/tex] .
nên: [tex]g'(x)=0<=>x=\left \{ -3;1;3 \right \}[/tex].
đồ thị f'(x) và đường thẳng y=x+1 cắt nhau tạo thành 2 miền kín, miền lớn bên trái và nhỏ bên phải.
diện tích miền bên trái:
[tex]S_1=\int_{-3}^{1}|f'(x)-(x+1)|dx=\int_{-3}^{1}(f'(x)-(x+1))dx> 0<=>\frac{g(1)}{2}>\frac{g(-3)}{2}<=>g(1)>g(-3)[/tex]
diện tích miền bên phải:
[tex]S_2=\int_{1}^{3}|f'(x)-(x+1)|dx=\int_{1}^{3}-(f'(x)-(x+1))dx> 0<=>\frac{g(1)}{2}>\frac{g(3)}{2}<=>g(1)>g(3)[/tex]
mà [tex]S_1>S_2=>g(3)>g(-3)[/tex].
vậy, g(1)>g(3)>g(-3).
ví dụ 2: cho hàm số y=f(x) có đồ thị f'(x) như hình vẽ,cắt trục hoành lần lượt tại a, b, c với a<b<c, biết f(c)<0. tìm số nghiệm của phương trình f(x)=0.
giải:
xét miền kín phía dưới trục Ox: [tex]S_1=\int_{a}^{b}\left |f'(x) \right |dx=\int_{a}^{b}-f'(x)dx> 0<=>f(a)>f(b)[/tex]
xét miền kín phía trên trục Ox: [tex]S_1=\int_{b}^{c}\left |f'(x) \right |dx=\int_{b}^{c}f'(x)dx> 0<=>f(c)>f(b)[/tex]
do diện tích miền trên lớn hơn diện tích miền dưới nên f(c)>f(a).
mà f(c)<0 nên suy ra f(a), f(b)<0.
lập bảng biến thiên, ta thấy phương trình f(x)=0 vô nghiệm.
