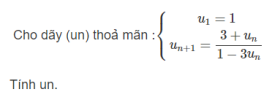Ngocloc2005Bài này mình làm theo công thức sẵn, hỏi tại sao lại làm thế thì hơi khó mong bạn thông cảm. Cùng với đó, mình không chắc đây là cách nhanh nhất nhé.
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Đặt [imath]x_{n+1} =x_{n} + 3y_n; y_{n+1} = -3x_n + y_n[/imath] với [imath]x_1=y_1=1 \Rightarrow x_2 = x_1 + 3y_1 = 4; y_2 = -3x_1 + y_1 = -2[/imath]
[imath]\Rightarrow x_{n+2} = x_{n+1} + 3y_{n+1} \Rightarrow 3y_{n+1} = x_{n+2} - x_{n+1}[/imath]
Vì [imath]y_{n+1} = -3x_n+y_n \Rightarrow 3y_{n+1} = -9x_n + 3y_{n}[/imath]
[imath]\Rightarrow x_{n+2} - x_{n+1} = - 9x_n + x_{n+1} - x_n[/imath]
[imath]\Rightarrow x_{n+2} - 2x_{n+1} + 10x_n = 0[/imath]
Xét phương trình đặc trưng: [imath]x^2-2x+10=0[/imath]
[imath]\Delta'=(-1)^2 - 10 = -9 < 0[/imath]
[imath]\Rightarrow x_n = \sqrt{10}^n \left( \alpha \cos \left ( n.\arccos \left (\dfrac{1}{\sqrt{10}} \right ) \right ) +\beta \sin \left ( n.\arccos \left (\dfrac{1}{\sqrt{10}} \right ) \right ) \right )[/imath]
Mà [imath]x_1=1;x_2=4[/imath]
[imath]\Rightarrow x_n = \sqrt{10}^n \left( \dfrac{-1}{5} \cos \left ( n.\arccos \left (\dfrac{1}{\sqrt{10}} \right ) \right ) +\dfrac{2}{5} \sin \left ( n.\arccos \left (\dfrac{1}{\sqrt{10}} \right ) \right ) \right )[/imath]
Giải tương tự với y ta được: [imath]\Rightarrow y_n = \sqrt{10}^n \left( \dfrac{2}{5} \cos \left ( n.\arccos \left (\dfrac{1}{\sqrt{10}} \right ) \right ) +\dfrac{1}{5} \sin \left ( n.\arccos \left (\dfrac{1}{\sqrt{10}} \right ) \right ) \right )[/imath]
Ta sẽ chứng minh quy nạp chỉ ra [imath]u_n=\dfrac{x_n}{y_n}[/imath]
Với [imath]n=1 \Rightarrow u_1=1[/imath] (đúng)
Giả sử [imath]u_k = \dfrac{x_k}{y_k}[/imath]
Ta có: [imath]u_{k+1} = \dfrac{3+u_{k}}{1-3u_{k}} =\dfrac{3+\dfrac{x_k}{y_k}}{1-3\dfrac{x_k}{y_k}} = \dfrac{x_k + 3y_k}{-3x_k + y_k} =\dfrac{x_{k+1}}{y_{k+1}}[/imath]
[imath]\Rightarrow u_k = \dfrac{ -\cos \left ( n.\arccos \left (\dfrac{1}{\sqrt{10}} \right ) \right ) +2\sin \left ( n.\arccos \left (\dfrac{1}{\sqrt{10}} \right ) \right ) }{2\cos \left ( n.\arccos \left (\dfrac{1}{\sqrt{10}} \right ) \right ) +\sin \left ( n.\arccos \left (\dfrac{1}{\sqrt{10}} \right ) \right )}[/imath]
Chúc bạn sớm hiểu được nội dung bài làm !!
Xin phép không tag link, bởi chắc không có link nào phù hợp bài này.
Bạn tham khảo thêm kiến thức mọi nguồn để biết cách làm TQ. Mình cũng bắt chước thôi ạ
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
