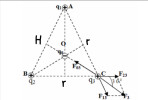
Vì 3 điện tích giống nhau, nên một điện tích cân bằng thì cả 3 điện tích sẽ cân bằng
Do đó mình sẽ xét lực tác dụng lên [imath]q_{3}[/imath]: [imath]\overrightarrow{F_{3}}=\overrightarrow{F_{13}}+\overrightarrow{F_{23}}[/imath]
View attachment 210241
Ta có: [imath]F_{13}=F_{23}=k\frac{q^{2}}{r^{2}}\Rightarrow F_{3}=2F_{13}.cos(30)=F_{13}.\sqrt{3}[/imath]
Để [imath]q_{3}[/imath] cân bằng thì cần 1 lực [imath]F_{03}[/imath] do [imath]q_{0}[/imath] tác dụng lên [imath]q_{3}[/imath] sao cho nó ngược chiều và có độ lớn bằng [imath]F_{3}[/imath]
[imath]\Rightarrow q_{0}<0[/imath]
xét tương tự với [imath]q_{1},q_{2}[/imath] thì [imath]q_{0}[/imath] nằm ở tâm tam giác ABC
Ta có [imath]CH=\frac{\sqrt{3}}{2}.r[/imath], [imath]CO=\frac{2}{3}CH=\frac{2}{3}.\frac{\sqrt{3}}{2}r=\frac{\sqrt{3}}{3}r[/imath]
Vậy [imath]F_{3}= F_{03}\Rightarrow \frac{k|q_{3}.q_{0}|}{(\frac{\sqrt{3}}{3}r)^{2}}[/imath] Ta sẽ tính được [imath]q_{0}[/imath]
Chúc bạn học tốt
Bạn xem thêm:
Chuyển động thẳng biến đổi đều
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.