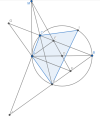
Gọi [imath]G[/imath] là giao điểm của [imath]AD[/imath] với [imath]BC[/imath], [imath]H[/imath] là giao điểm của [imath]AC[/imath] với [imath]BD[/imath].
Gọi [imath]E',F'[/imath] là 2 điểm trên [imath]BC,BD[/imath] sao cho [imath]AE' \parallel BD, AF' \parallel BC[/imath].
Áp dụng định lý Ta-lét ta có: [imath]\dfrac{E'C}{E'B}=\dfrac{AC}{AH},\dfrac{BF'}{F'D}=\dfrac{GA}{AD}[/imath]
Mặt khác, [imath]\Delta GAC \sim \Delta GDA \Rightarrow \dfrac{GA}{GC}=\dfrac{GD}{GA}=\dfrac{AD}{AC}[/imath]
[imath]\Rightarrow \dfrac{GD}{GC}=\dfrac{GA}{GC}\cdot \dfrac{GD}{GA}=(\dfrac{AD}{AC})^2[/imath]
[imath]\Rightarrow \dfrac{E'C}{E'B} \cdot \dfrac{BF'}{F'D} \cdot \dfrac{DG}{CG}=\dfrac{AC}{AH}\cdot \dfrac{GA}{AD} \cdot (\dfrac{AD}{AC})^2=\dfrac{GA}{AH} \cdot \dfrac{AD}{AC}[/imath]
Lại có [imath]\Delta GAC \sim \Delta HAD \Rightarrow \dfrac{AD}{AC}=\dfrac{AH}{AG} \Rightarrow \dfrac{E'C}{E'B} \cdot \dfrac{BF'}{F'D} \cdot \dfrac{DG}{CG}=1[/imath]
Áp dụng định lý Menelaus cho [imath]\Delta BCD[/imath] ta được [imath]G,E',F'[/imath] thẳng hàng.
Mà [imath]AE \parallel BD, AF \parallel BC \Rightarrow AEBF[/imath] là hình bình hành [imath]\Rightarrow E',O,F'[/imath] thẳng hàng và [imath]E'O=OF'[/imath](1)
Từ đó [imath]E',F'[/imath] là giao điểm của [imath]GO[/imath] với [imath]BC,BD \Rightarrow E \equiv E',F \equiv F'[/imath]
Từ (1) ta có đpcm.
Nếu còn thắc mắc chỗ nào bạn hãy trả lời dưới topic này để được hỗ trợ nhé. Chúc bạn học tốt ^^
Ngoài ra, bạn tham khảo kiến thức tại topic này nha
Ôn tập toán các dạng bài hình học 9
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.


