[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Bài 7 (2,5 điểm)
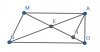
Từ điểm M nằm ngoài đường tròn (O;R) vẽ hai tiếp tuyến MA, MB (A, B là hai tiếp điểm)
a) Tính góc MAO và chứng minh góc MAB = góc MBA
b) Đường thẳng vuông góc với OA tại O cắt AB và MB lần lượt tại I.S
= Chứng minh : tam giác SOM cân ở S và SI + SO = MB
c) Gọi G là đối xứng của O qua S. MO cắt AG ở E và cắt AB ở H. Chứng minh : EH.EO<[tex]EG^{2}[/tex]
Cho em hỏi câu c bài này chứng minh sao ạ. Em cảm ơn
Từ điểm M nằm ngoài đường tròn (O;R) vẽ hai tiếp tuyến MA, MB (A, B là hai tiếp điểm)
a) Tính góc MAO và chứng minh góc MAB = góc MBA
b) Đường thẳng vuông góc với OA tại O cắt AB và MB lần lượt tại I.S
= Chứng minh : tam giác SOM cân ở S và SI + SO = MB
c) Gọi G là đối xứng của O qua S. MO cắt AG ở E và cắt AB ở H. Chứng minh : EH.EO<[tex]EG^{2}[/tex]
Cho em hỏi câu c bài này chứng minh sao ạ. Em cảm ơn