- 29 Tháng sáu 2017
- 2,299
- 4,069
- 546
- 25
- Cần Thơ
- Đại Học Cần Thơ
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
- Gần đến kí thi học kì 1 rồi nên mình lập topic này để các bạn cũng cố lại kiến thức và sẽ có những đề thi để chúng ta luyện tập.
CHỦ ĐỀ 1: ÔN LẠI LÝ THUYẾT VÀ CÁC DẠNG BÀI TẬP CƠ BẢN DAO ĐỘNG ĐIỀU HÒA
I. Nhắc lại kiến thức
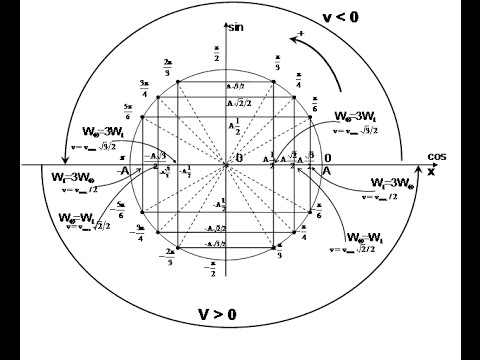
- Phương trình dao động: x = [tex]Acos(\omega t + \varphi )[/tex]
Trong đó : + A là biên độ dao động (A > 0). Nó là độ lệch cực đại của vật; đơn vị m, cm
+ [tex]\omega t+\varphi[/tex] là pha của dao động tại thời điểm t; đơn vị rad.
+ [tex]\varphi[/tex] là pha ban đầu của dao động; đơn vị rad.
- Phương trình của vận tốc: [tex]v=x'=-\omega Asin(\omega t+\varphi )[/tex]
- Phương trình của gia tốc: [tex]a=v'=x''=-\omega A^{2}cos(\omega t+\varphi )[/tex]
* Một số công thức cơ bản:
+ [tex]\omega =2\pi f=\frac{2\pi }{T}[/tex] ( rad/s)
+ [tex]f=\frac{1}{T}=\frac{\omega }{2\pi }[/tex] (Hz)
+ [tex]T=\frac{1}{f}=\frac{2\pi }{\omega }[/tex]
+ Chiều dài của quỹ đạo: là một đoạn thẳng dài (L=2A)
II. Ví dụ minh họa
ĐỀ: Một vật dao động điều hòa với phương trình [tex]x = 8cos(4\pi t-\frac{\pi }{4})[/tex] , với x tính bằng cm và t tính bằng s. Hãy xác định
1. biên độ dao động, chiều dài của quỹ đạo?
2. tần số góc, chu kì và tần số?
3. pha ban đầu, pha của dao động là?
4. biểu thức vận tốc?
5. biểu thức gia tốc?
6. Đặt vật dao động bên cạnh một vật thứ hai thì thấy li độ dao động của chúng có mối liên hệ: [tex]16x1^{2} + 9x2^{2} = 15^{2}[/tex]. Khi x1 = 3 cm và v1= [tex]20\sqrt{22}[/tex] thì vận tốc của vật thứ hai có độ lớn bằng bao nhiêu?
BÀI GIẢI
Ta có phương trình dao động tổng quát là: x= [tex]Acos(\omega t+\varphi )[/tex]
1. Biên độ dao động A=8cm
2. Các đại lượng
+ Tần số góc: [tex]\omega = 4\pi[/tex] rad/s
+ Chu kì dao động: [tex]T=\frac{2\pi }{\omega } = 0,5 s[/tex]
+ Tần số : [tex]f=\frac{1}{T}=\frac{\omega }{2\pi } = 2 Hz[/tex]
3. Pha ban đầu: [tex]\varphi =\frac{-\pi }{4}[/tex]; pha của dao động: [tex](\omega t+\varphi ) = (4\pi t-\frac{\pi }{4})[/tex]
4. Biểu thức vận tốc:
[tex]v=x'=-\omega Asin(\omega t+\varphi )=-4\pi .8sin(4\pi t-\frac{\pi }{4})= 32\pi cos(4\pi t+\frac{\pi }{4})[/tex]
5. Biểu thức gia tốc:
[tex]a=v'=x''= -(4\pi )^{2}8sin(4\pi t-\frac{\pi }{4})= (4\pi )^{2}8cos(4\pi t+\frac{3\pi }{4})[/tex]
6. Đề bài cho mối liên hệ: [tex]16x1^{2}+ 9x2^{2}=15^{2}[/tex]. Vậy chúng ta muốn tìm được vận tốc của vật thứ hai chúng ta cần đạo hàm mối liên hệ đó đế xuất hiện v2.
+ Lấy đạo hàm của 2 vế ta được:
[tex]16.2.x_{1}v_{1} + 9.2.x_{2}.v_{2}=0 => v_{2}= - \frac{16x_{1}v_{1}}{9x_{2}} => \left | v_{2} \right | = 166 cm/s[/tex]
Xem thêm:
[Vật lí 7] HỆ THỐNG MỤC MỤC CÁC LỚP
[Vật lí 8] HỆ THỐNG MỤC MỤC CÁC LỚP
[Vật lí 9] HỆ THỐNG MỤC MỤC CÁC LỚP
[Vật lí 10] HỆ THỐNG MỤC MỤC CÁC LỚP
[Vật lí 11] HỆ THỐNG MỤC MỤC CÁC LỚP
[Vật lí 12] HỆ THỐNG MỤC MỤC CÁC LỚP
CHỦ ĐỀ 1: ÔN LẠI LÝ THUYẾT VÀ CÁC DẠNG BÀI TẬP CƠ BẢN DAO ĐỘNG ĐIỀU HÒA
I. Nhắc lại kiến thức
- Phương trình dao động: x = [tex]Acos(\omega t + \varphi )[/tex]
Trong đó : + A là biên độ dao động (A > 0). Nó là độ lệch cực đại của vật; đơn vị m, cm
+ [tex]\omega t+\varphi[/tex] là pha của dao động tại thời điểm t; đơn vị rad.
+ [tex]\varphi[/tex] là pha ban đầu của dao động; đơn vị rad.
- Phương trình của vận tốc: [tex]v=x'=-\omega Asin(\omega t+\varphi )[/tex]
- Phương trình của gia tốc: [tex]a=v'=x''=-\omega A^{2}cos(\omega t+\varphi )[/tex]
* Một số công thức cơ bản:
+ [tex]\omega =2\pi f=\frac{2\pi }{T}[/tex] ( rad/s)
+ [tex]f=\frac{1}{T}=\frac{\omega }{2\pi }[/tex] (Hz)
+ [tex]T=\frac{1}{f}=\frac{2\pi }{\omega }[/tex]
+ Chiều dài của quỹ đạo: là một đoạn thẳng dài (L=2A)
II. Ví dụ minh họa
ĐỀ: Một vật dao động điều hòa với phương trình [tex]x = 8cos(4\pi t-\frac{\pi }{4})[/tex] , với x tính bằng cm và t tính bằng s. Hãy xác định
1. biên độ dao động, chiều dài của quỹ đạo?
2. tần số góc, chu kì và tần số?
3. pha ban đầu, pha của dao động là?
4. biểu thức vận tốc?
5. biểu thức gia tốc?
6. Đặt vật dao động bên cạnh một vật thứ hai thì thấy li độ dao động của chúng có mối liên hệ: [tex]16x1^{2} + 9x2^{2} = 15^{2}[/tex]. Khi x1 = 3 cm và v1= [tex]20\sqrt{22}[/tex] thì vận tốc của vật thứ hai có độ lớn bằng bao nhiêu?
BÀI GIẢI
Ta có phương trình dao động tổng quát là: x= [tex]Acos(\omega t+\varphi )[/tex]
1. Biên độ dao động A=8cm
2. Các đại lượng
+ Tần số góc: [tex]\omega = 4\pi[/tex] rad/s
+ Chu kì dao động: [tex]T=\frac{2\pi }{\omega } = 0,5 s[/tex]
+ Tần số : [tex]f=\frac{1}{T}=\frac{\omega }{2\pi } = 2 Hz[/tex]
3. Pha ban đầu: [tex]\varphi =\frac{-\pi }{4}[/tex]; pha của dao động: [tex](\omega t+\varphi ) = (4\pi t-\frac{\pi }{4})[/tex]
4. Biểu thức vận tốc:
[tex]v=x'=-\omega Asin(\omega t+\varphi )=-4\pi .8sin(4\pi t-\frac{\pi }{4})= 32\pi cos(4\pi t+\frac{\pi }{4})[/tex]
5. Biểu thức gia tốc:
[tex]a=v'=x''= -(4\pi )^{2}8sin(4\pi t-\frac{\pi }{4})= (4\pi )^{2}8cos(4\pi t+\frac{3\pi }{4})[/tex]
6. Đề bài cho mối liên hệ: [tex]16x1^{2}+ 9x2^{2}=15^{2}[/tex]. Vậy chúng ta muốn tìm được vận tốc của vật thứ hai chúng ta cần đạo hàm mối liên hệ đó đế xuất hiện v2.
+ Lấy đạo hàm của 2 vế ta được:
[tex]16.2.x_{1}v_{1} + 9.2.x_{2}.v_{2}=0 => v_{2}= - \frac{16x_{1}v_{1}}{9x_{2}} => \left | v_{2} \right | = 166 cm/s[/tex]
Xem thêm:
[Vật lí 7] HỆ THỐNG MỤC MỤC CÁC LỚP
[Vật lí 8] HỆ THỐNG MỤC MỤC CÁC LỚP
[Vật lí 9] HỆ THỐNG MỤC MỤC CÁC LỚP
[Vật lí 10] HỆ THỐNG MỤC MỤC CÁC LỚP
[Vật lí 11] HỆ THỐNG MỤC MỤC CÁC LỚP
[Vật lí 12] HỆ THỐNG MỤC MỤC CÁC LỚP