 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
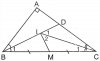
Cho mình hỏi là sao tính BC = 10cm đc zNgày 26 làm bài 26 cho đẹp
View attachment 80556
a) Kéo dài BI cắt AC ở D
Áp dụng định lý Pi-ta-go tính được BC = 10 (cm)
Áp dụng tính chất tia phân giác trong tam giác để tính DA = 3(cm); DC = 5(cm)
Xét tam giác IDC và tam giác IMC bằng nhau => [tex]\angle I1=\angle I2=\angle B1+\angle C1[/tex] (tính chất góc ngoài của tam giác)
Mà: [tex]\angle B1+\angle C1=45^{o}\\ \Rightarrow \angle I1=\angle I2=45^{0}\Rightarrow \angle BIM=180^{o}-45^{o}-45^{o}=90^{o}[/tex]
b) Theo định lý Pi-ta-go ta có: [tex]BC^2=AB^2+AC^2[/tex](1)
Mà: [tex]\angle ADB=\angle BMI[/tex] (cùng phụ với [tex]\angle B1[/tex]
=> góc DIC = góc MIC
=> tam giác MIC = tam giác DIC
=> MC = DC = [tex]\frac{1}{2}BC[/tex]
Áp dụng tính chất tia phân giác ta có:
[tex]\frac{AD}{DC}=\frac{AB}{BC}\Rightarrow \frac{AD}{AB}=\frac{DC}{BC}=\frac{1}{2}\\ \Rightarrow AB+BC=2(AD+DC)=2AC[/tex] (2)
Từ (1) và (2) ta có hệ phương trình:
[tex]\left\{\begin{matrix} BC^2=AB^2+AC^2 & \\ AB+BC=2AC & \end{matrix}\right.[/tex]
giải hệ ta có ba cạnh tỉ lệ với 3; 4 ;5
Áp dụng định lý pi-ta -go đó bạn:Cho mình hỏi là sao tính BC = 10cm đc z
À hình như bạn nhầm bài 25 sag 26 thì phảiÁp dụng định lý pi-ta -go đó bạn:
[tex]BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10(cm)[/tex]
chết, mình nhầm, định làm bài 25 mà mắt kém nhìn sang bài 26, xin lỗi bạnÀ hình như bạn nhầm bài 25 sag 26 thì phải
Ko sao đâu thì lỡ rùi nay ngày 26 lèm bài 26 lun ik cho đẹpchết, mình nhầm, định làm bài 25 mà mắt kém nhìn sang bài 26, xin lỗi bạn
À hình như bạn nhầm bài 25 sag 26 thì phải
Bạn cho mk hỏi là giải hệ như nào để ra 3 cạnh tỉ lệ là 3,4,5 vậyNgày 26 làm bài 25 cho đẹp
View attachment 80556
a) Kéo dài BI cắt AC ở D
Áp dụng định lý Pi-ta-go tính được BC = 10 (cm)
Áp dụng tính chất tia phân giác trong tam giác để tính DA = 3(cm); DC = 5(cm)
Xét tam giác IDC và tam giác IMC bằng nhau => [tex]\angle I1=\angle I2=\angle B1+\angle C1[/tex] (tính chất góc ngoài của tam giác)
Mà: [tex]\angle B1+\angle C1=45^{o}\\ \Rightarrow \angle I1=\angle I2=45^{0}\Rightarrow \angle BIM=180^{o}-45^{o}-45^{o}=90^{o}[/tex]
b) Theo định lý Pi-ta-go ta có: [tex]BC^2=AB^2+AC^2[/tex](1)
Mà: [tex]\angle ADB=\angle BMI[/tex] (cùng phụ với [tex]\angle B1[/tex]
=> góc DIC = góc MIC
=> tam giác MIC = tam giác DIC
=> MC = DC = [tex]\frac{1}{2}BC[/tex]
Áp dụng tính chất tia phân giác ta có:
[tex]\frac{AD}{DC}=\frac{AB}{BC}\Rightarrow \frac{AD}{AB}=\frac{DC}{BC}=\frac{1}{2}\\ \Rightarrow AB+BC=2(AD+DC)=2AC[/tex] (2)
Từ (1) và (2) ta có hệ phương trình:
[tex]\left\{\begin{matrix} BC^2=AB^2+AC^2 & \\ AB+BC=2AC & \end{matrix}\right.[/tex]
giải hệ ta có ba cạnh tỉ lệ với 3; 4 ;5
bạn quy tất cả về một cái là được mà, giả sử quy tất cả về AC ấyBạn cho mk hỏi là giải hệ như nào để ra 3 cạnh tỉ lệ là 3,4,5 vậy

