[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
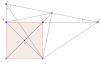
Bài 1: Cho hình vuông ABCD; trên tia đối tia BA lấy E; trên tia đối tia CB lấy F sao cho AE=CF.
a)CM: [tex]\Delta EDF[/tex] vuông cân
b) Gọi O là giao điểm hai đường chéo AC và BD. Gọi I la trung điểm của EF. CM: ba điểm O,C,I thẳng hàng.
Bài 2: Cho hình bình hành ABCD có (AC>BD); hình chiếu góc của góc C lên AB,AD lần lượt ở E và F.
a)CM: CE.CD=CB.CF và [tex]\Delta ABC \sim \Delta FCE[/tex].
b)Gọi H và K là hình chiếu vuông góc của góc D và góc B lên AC. CM:[tex]AB.AE+AD.AF=AC^{2}[/tex]
a)CM: [tex]\Delta EDF[/tex] vuông cân
b) Gọi O là giao điểm hai đường chéo AC và BD. Gọi I la trung điểm của EF. CM: ba điểm O,C,I thẳng hàng.
Bài 2: Cho hình bình hành ABCD có (AC>BD); hình chiếu góc của góc C lên AB,AD lần lượt ở E và F.
a)CM: CE.CD=CB.CF và [tex]\Delta ABC \sim \Delta FCE[/tex].
b)Gọi H và K là hình chiếu vuông góc của góc D và góc B lên AC. CM:[tex]AB.AE+AD.AF=AC^{2}[/tex]
Last edited by a moderator: