a)

- Thấy AE = FD (cùng bằng FM). Dễ dàng chứng minh ∆ADE = ∆DCF (c - g - c)
₍₁₎
⇒ ∠ADE = ∠DCF ⇒ ∠ADE = 90° - ∠DFC
⇒ ∠ADE + ∠DFC = 90° ⇒ ∠DKF = 90° (DE ⋂ CF = {K})
⇒ DE ⊥ CF (đpcm)
₍₁₎ ⇒ DE = CF (đpcm)
b)
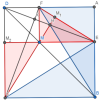
- Tương tự câu a), chứng minh
∆AFB = ∆BEC (c - g - c) ⇒ CE ⊥ BF
- Trong ∆CEF, thấy ED ⊥ CF và FB ⊥ EC ⇒ H là trực tâm ∆CEF (ED ⋂ FB = {H})
- Thấy ME = M₂C (cùng bằng EB) (MM₂ ⊥ CD | M₂ ∈ CD).
Dễ dàng chứng minh ∆MFE = ∆M₂MC (c - g - c)
- Có: ∆M₁FM ᔕ ∆MFE (g - g) (MM₁ ⊥ EF | M₁ ∈ EF) ⇒ ∆M₂MC ᔕ ∆M₁FM
⇒ ∠M₂CM = ∠M₁MF
- Có: ∠M₂MC + ∠M₂MF + ∠FMM₁ = ∠M₂MC + 90° + ∠M₂CM
= ∠M₂MC + ∠MM₂C + ∠M₂CM = 180°
⇒ ∠CMM₁ = 180° ⇒ C, M, M₁ thẳng hàng
mà MM₁ ⊥ EF ⇒ CM ⊥ EF
mà H là trực tâm ∆CEF ⇒ CM, FB, ED đồng quy (đpcm)
c)

- Có: 4AE.AF ≤ (AE + AF)² = BC² ⇒ S_AEMF = AE.AF ≤ BC²/4.
Đẳng thức xảy ra ⇔ AE = AF ⇔ M là trung điểm của BD
Vậy min S_AEMF = BC²/4, đạt được khi M là trung điểm của BD
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.




