[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
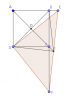
1/ Cho hình vuông ABCD, trên tia đối tia BA lấy E, trên tia đối tia CB lấy F sao cho AE=CF.
a)chứng minh:tam giác EDF vuông cân
b)Gọi O là giao điểm của 2 đường chéo AC và BD. Gọi I là trung điểm EF.Chứng minh:O,C,I thẳng hàng
2/ Cho tam giác ABC vuông cân tại A.Các điểm D,E theo thứ tự di chuyển trên AB,AC sao cho BD=AE. Xác định vị trí điểm D,E sao cho:
a)DE có độ dài nhỏ nhất
b)Tứ giác BDEC có diện tích nhỏ nhất
3/ Cho đoạn thẳng AB, M là điểm nằm giữa A và B. Trên cùng nửa mặt phẳng bờ AB kẻ các hình vuông ACDM và MNPB.Gọi K là giao điểm của CP và NB.CMR:khi M di chuyển giữa A và B thì khoảng cách từ K đến AB không đổi
a)chứng minh:tam giác EDF vuông cân
b)Gọi O là giao điểm của 2 đường chéo AC và BD. Gọi I là trung điểm EF.Chứng minh:O,C,I thẳng hàng
2/ Cho tam giác ABC vuông cân tại A.Các điểm D,E theo thứ tự di chuyển trên AB,AC sao cho BD=AE. Xác định vị trí điểm D,E sao cho:
a)DE có độ dài nhỏ nhất
b)Tứ giác BDEC có diện tích nhỏ nhất
3/ Cho đoạn thẳng AB, M là điểm nằm giữa A và B. Trên cùng nửa mặt phẳng bờ AB kẻ các hình vuông ACDM và MNPB.Gọi K là giao điểm của CP và NB.CMR:khi M di chuyển giữa A và B thì khoảng cách từ K đến AB không đổi
Last edited by a moderator: