không ạ.
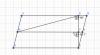
AD=2AB => MNCD là hình thoi
Hèn chi mình ngẫm hoài k thấy câu c) có bằng đâu mà cm -,-
Thì ra đọc đề sai :<
a) (Câu này chứng minh thêm 1 câu nữa.)
Mà ta có AD = 2AB
$\Rightarrow$ AB = AM = MD
Ta có MN // AB // CD, AM = MD
$\Rightarrow$ MN là đường trung bình.
$\Rightarrow$ MN = AB = CD = BN = CN = AM = MD
$\Rightarrow$ MNCD là hình thoi.
b) (Thôi tốt nhất nên bỏ hết đi.)
Ta có F thuộc MN, F thuộc CE, MN vuông góc với CE
$\Rightarrow$ EF = FC.
Ta có MF vừa là đường trung tuyến vừa là đường cao
$\Rightarrow$ MEC là tam giác cân tại M.
Xét tam giác EMF và tam giác CMF
- MF là cạnh chung.
- EF = FC (cmt)
$\Rightarrow$ EMF = CMF (hai cạnh góc vuông)
$\Rightarrow$ góc MEF = MCF, góc M1 = M2
Mà ta có MNCD là hình thoi:
$\Rightarrow$ góc MCD = 45 độ
$\Rightarrow$ góc MCF = 45 độ
$\Rightarrow$ góc MEF = 45 độ
Mà ta có M1 + MCF = 90 độ
M2 + MEF = 90 độ
$\Rightarrow$ M1 = M2 = 45 độ
$\Rightarrow$ M1 + M2 = 90 độ
$\Rightarrow$ EMC là tam giác vuông cân.
c) Vì EMC là tam giác vuông cân
$\Rightarrow$ MF = EF = CF
$\Rightarrow$ AEM = 45 độ.
Ta có F1 = 90 độ, MF = EF
$\Rightarrow$ MEF là tam giác vuông cân.
Ta có F2 = 90 độ, MF = CF
$\Rightarrow$ MCF là tam giác vuông cân.
Ta có MNCD là hình thoi
$\Rightarrow$ M4 = M2
Mà M2 = AEM
$\Rightarrow$ M4 + M2 = 2AEM
Ta có M4 + M2 = M
Mà M = A (cmn)
$\Rightarrow$ BAD = 2AEM
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
