Bài 6:
Sai đề rồi nhé. Phải là $HE$ đi qua trung điểm $AC$ nhé.
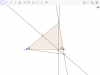
Gọi giao điểm của $EH$ và $AC$ là $F$
Dễ thấy: $\widehat{ABC}=2 \widehat{ACB}=2\widehat{BEH} \\\Rightarrow \widehat{ACH}=\widehat{BHE}$.
Mặt khác: $\widehat{FHC}=\widehat{BHE}$.
Nên $\widehat{ACH}=\widehat{FHC}$.
Do đó tam giác $FCH$ cân tại $F$ nên $FC=FH$.
Mặt khác: $90^0-\widehat{ACH}=90^0-\widehat{FHC} \\\Leftrightarrow \widehat{CAH}=\widehat{FHA}$.
Nên cũng suy ra được $AF=FH$.
Do đó $CF=HF=AF$ hay $F$ là trung điểm $AC$.
Bài 7:
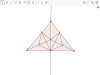
a)Dễ thấy $KG,KH$ là đường trung bình của các tam giác $\triangle BIC$.
Do đó $KG//IC,KH//IB$ nên $IGKH$ là hình bình hành do đó $\widehat{IGK}=\widehat{IHK}(1)$.
Mặt khác dễ dàng chứng minh $\triangle BEI \sim \triangle CEI$ mà $G,H$ là trung điểm nên $\widehat{EGI}=\widehat{FHI}(2)$.
Cộng vế theo vế $(1)+(2)$ ta sẽ thu được $\widehat{EGK}=\widehat{FHK}$.
b)Tam giác $BEI$ vuông có $EG$ là đường trung tuyến nên $EG=\dfrac{1}{2}BI$.
Mặt khác $KH$ là đường trung bình nên $KH=\dfrac{1}{2}BI=EG$.
Chứng minh tương tự cũng có: $GK=FH$.
Mặt khác $\widehat{EGK}=\widehat{FHK}$
Nên $\triangle EGK=\triangle KHF \Rightarrow KE=KF$.
Do đó đường trung trực của $EF$ đi qua $K$.
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
