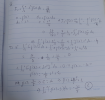[imath]\displaystyle \int \limits_0^1 x^3f(x)= \dfrac{x^4}{4}f(x)\Big|^1_0 -\displaystyle \int \limits_0^1 \dfrac{x^4f'(x)}{4}[/imath]
[imath]=\dfrac{3}{20}-\displaystyle \int \limits_0^1 \dfrac{x^4f'(x)}{4}=\dfrac{37}{180}[/imath]
[imath]\Rightarrow \displaystyle \int \limits_0^1 x^4f'(x)=\dfrac{-2}{9}[/imath]
[imath]\left(\dfrac{-2}{9}\right)^2=\left(\displaystyle \int \limits_0^1 x^4f(x)\right)\le \displaystyle \int \limits_0^1 x^8\displaystyle \int \limits_0^1 f'(x)^2=\dfrac{4}{81}[/imath]
Dấu "=" xảy ra khi và chỉ khi [imath]f'(x)=kx^4[/imath]
[imath]\Rightarrow f(x)=\dfrac{kx^5}{5}+c[/imath]
[imath]\Rightarrow f(1)=\dfrac{k}{5}+c=\dfrac{3}5\Rightarrow c=\dfrac{3}5-\dfrac{k}{5}[/imath]
[imath]\displaystyle \int \limits_0^1 x^3\left(\dfrac{kx^5}{5}+\dfrac{3}5-\dfrac{k}{5}\right)=\dfrac{k}{45}+\dfrac{3}{20}-\dfrac{k}{20}=\dfrac{37}{180}\Rightarrow k=-2[/imath]
[imath]\Rightarrow f(x)=-\dfrac25x^5+1[/imath]
[imath]\Rightarrow \displaystyle \int \limits_0^1 [f(x)-3]=\dfrac{-31}{15}[/imath]
Có gì khúc mắc bạn hỏi lại nhé
Ngoài ra bạn tham khảo thêm tại
Chinh phục kì thi THPTQG môn Toán 2022
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
