B
binhhiphop
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
1/ Cho
 và
và
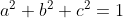
CMR:

2/ Phân tích đa thức thành nhân tử:


3/ Tìm số dư R khi chia
 cho
cho

4/ Tìm
 để
để

5/ CMR nếu
 và
và
 là các số dương thì
là các số dương thì

6/ CMR nếu
 và
và
 là các số dương thì
là các số dương thì

7/ Cho
 và
và

Tính theo a, b


8/
 có là tích của hai số tự nhiên liên tiếp không?
có là tích của hai số tự nhiên liên tiếp không?
Thêm 1 Câu HÌnh CHO đủ VỊ
Cho tam giác ABC vuông tại A. Về phía ngoài tam giác dựng hình vuông BCDE. AD, AE lần lượt cắt BC tại M và N. Chứng minh rằng [TEX]MN^2=CM*BN[/TEX]
CMR:
2/ Phân tích đa thức thành nhân tử:
3/ Tìm số dư R khi chia
4/ Tìm
5/ CMR nếu
6/ CMR nếu
7/ Cho
Tính theo a, b
8/
Thêm 1 Câu HÌnh CHO đủ VỊ
Cho tam giác ABC vuông tại A. Về phía ngoài tam giác dựng hình vuông BCDE. AD, AE lần lượt cắt BC tại M và N. Chứng minh rằng [TEX]MN^2=CM*BN[/TEX]
Last edited by a moderator:

