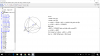
Cho tam giác ABC có 3 góc nhọn nội tiếp (O;R). Điểm M di động trên cung BC. Từ M kẻ các đường thằng MH, MK lần lượt vuông góc vs AB, AC ( H thuộc AB, K thuộc AC). CM: tam giác MBC đồng dạng với tam giác MHK.
Hình bạn tự vẽ, M di chuyển trên cung lớn và cung nhỏ thì cách làm đều tương tự nhau nha.
Bạn chứng minh đc:
+ T/g ABMC nội tiếp:
[tex]\Rightarrow \left\{\begin{matrix} \widehat{CAM}=\widehat{CBM}\\ \widehat{BAM}=\widehat{BCM} \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} \widehat{KAM}=\widehat{CBM}(1)\\ \widehat{HAM}=\widehat{BCM} (2) \end{matrix}\right.[/tex]
+ Tứ giác AHMK nội tiếp:
[tex]\Rightarrow \left\{\begin{matrix} \widehat{KHM}=\widehat{KAM}\\ \widehat{MHK}=\widehat{MAH} \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} \widehat{KHM}=\widehat{KAM}(3)\\ \widehat{MKH}=\widehat{MAH} (4) \end{matrix}\right.[/tex]
+ Từ (1) và (3) [tex]\Rightarrow \widehat{KHM}=\widehat{CBM}[/tex]
+ Từ (2) và (4) [tex]\Rightarrow \widehat{BCM}=\widehat{MKH}[/tex]
Từ đây [tex]\Rightarrow \Delta MBC\sim \Delta MHK[/tex]
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
