Toán toán 9, hình học đường tròn

[Trọngg Nhânn]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

bài này sao ạ, a vs b thì đc r còn câu c vs d ấy ạ
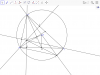
Cho đường tròn tâm 0, dây BC cố định,Gọi A là điểm cố định trên cung BC lớn. Gọi AD,BE,CF là đường cao và H là trực tâm
a.CM:BCEF, AEHF nội tiếp
b.CM:BF.AB+CE.CA=BC.BC
c.M là trung điểm của BC.G là trọng tâm.CM:diện tích tam giác AHG= 2lần diện tích tam giác AGO
d.Tìm vị trí A để DH.DA đạt giá trị lớn nhất

 

[Nguyễn Xuân Hiếu]

c) Kẻ đường kính $AL$.
Ta có: $CL \perp AC$ mà $BH \perp AC$.
Nên: $BH//CL$.
CMTT $\Rightarrow BL//CH$.
Do đó $BHCL$ là hbh.
Mà $M$ là trung điểm $BC$ nên $H,M,L$ thằng hàng.
Ta có: $OA=OL;MH=ML$ nên $OM$ là đường trung bình của tam giác $AHL$.
Gọi giao điểm của $AM$ với $OH$ là $G'$.
Ta có: $\dfrac{GA}{GM}=\dfrac{AH}{OM}=2$.
Do đó $G'$ là trọng tâm hay $G'$ trùng $G$.
Xét tam giác $AHO$ có $GH=2OG$ nên: $S_{\triangle AHG}=2S_{\triangle AGO}$.
d) Dễ dàng chứng minh $\triangle DHC \sim \triangle DBA$
Do đó: $DH.AD=DC.DB \leq \dfrac{(DC+DB)^2}{4}=\dfrac{BC^2}{4}=const$.
Dấu '=' khi $BD=CD$ hay $A$ là điểm chính giữa cung $BC$.