[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
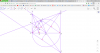
cho (O;R) có AB là đường kính .vẽ các tiếp tuyến Ax,By của (O) ,trên (O) lấy 1 điểm C sao cho AC<BC . tiếp tuyến tại C của (O) cắt Ax, By lần lượt tại E,F
a, CM EF=AE+BE
b. BC cắt Ax tại D .cm AD^2=DC.BD
c, gọi I là giao điểm của OD và AC , H là giao điểm của OE và AC , tia DH cắt AB tại K .CM IK//AD
d, IK giao EO tại M . CM A,M,F thẳng hàng
a, CM EF=AE+BE
b. BC cắt Ax tại D .cm AD^2=DC.BD
c, gọi I là giao điểm của OD và AC , H là giao điểm của OE và AC , tia DH cắt AB tại K .CM IK//AD
d, IK giao EO tại M . CM A,M,F thẳng hàng