N
nhung20020929
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
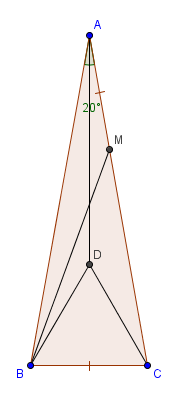
1)Cho tam giác $ABC$ có $\hat{A} =20^o$ , $\hat{B}=80^o$. Trên cạnh $AC$ lấy điểm $M$ sao cho $AM=BC$. Tính góc $BMC$
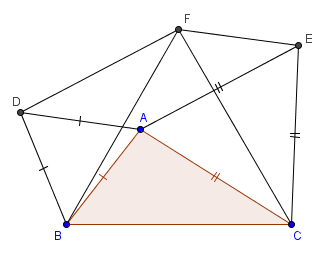
2)Lấy 2 cạnh $AB$ và $AC$ của $\triangle ABC$ ($\hat{A}\neq 60^o$) dựng ra phía ngoài góc $A$ 2 tam giác đều $ABD$ và $ACE$. Lấy $AD$ và $AE$ làm hai cạnh dựng hình bình hành $ADFE$. CMR $\triangle FBC$ đều
Giúp mình nhá cám ơn các bạn nhiều
2)Lấy 2 cạnh $AB$ và $AC$ của $\triangle ABC$ ($\hat{A}\neq 60^o$) dựng ra phía ngoài góc $A$ 2 tam giác đều $ABD$ và $ACE$. Lấy $AD$ và $AE$ làm hai cạnh dựng hình bình hành $ADFE$. CMR $\triangle FBC$ đều
Giúp mình nhá cám ơn các bạn nhiều
Last edited by a moderator: