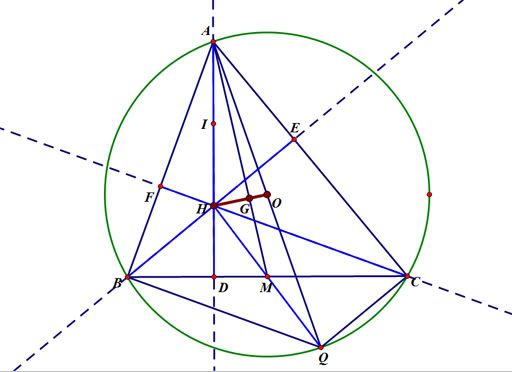
Chứng minh đường thẳng Euler, đường tròn Euler, và định lý Euler
Mình sẽ giúp bạn chứng minh lần lượt cả 3 cái luôn: Đường thẳng, Đường tròn, Định lý. Nhiều hơn cũng không sao ha ^^!, bạn tham khảo:
1. Chứng minh đường thẳng Euler
Cách 1:
Vẽ [tex]\large\Delta[/tex]ABC có giao điểm ba đường cao AD, BE, CF là H. G là trọng tâm của [tex]\Delta[/tex]ABC.
Từ B vẽ đường thẳng song song với HC, từ C vẽ đường thẳng song song với HB, chúng cắt nhau tại Q.
Gọi M là giao điểm của HQ và BC.
Xét tứ giác HCQB ta có :
[tex]\{ \begin BH// CQ (gt) \\BQ//CH (gt)[/tex]
\Rightarrow Tứ giác HCQB là hình bình hành vì có 2 cặp cạnh đối song song
\Rightarrow MB = MC và MH = MQ (tính chất đường chéo hình bình hành)
Xét [tex]\Delta[/tex]ABC có AM là đường trung tuyến (MB=MC):
Mà G là trọng tâm [tex]\Delta[/tex]ABC (gt)
\Rightarrow[tex]MG=\frac{1}{3}AM[/tex]
Xét [tex]\Delta[/tex]AHQ có AM là đường trung tuyến (MH=MQ)
Mà [tex]MG=\frac{1}{3}AM[/tex] (cmt)
\Rightarrow G là trọng tâm [tex]\Delta[/tex]AHQ
Ta có HO là đường trung tuyến (OA=OQ=R)
\RightarrowG [tex]\in\[/tex] HO.
======
Mình không rõ lớp 8 học đường tròn chưa, nên các kiến thức như góc nội tiếp chắn nửa đường tròn là góc vuông thì chắc là bạn chưa biết (nếu bạn học lớp 8)
. Cách chứng minh thì như trên. Không chứng minh song song được thì đành tự vẽ ra thôi ^^!
======
Cách 2:
CM: HCQB là hình bình hành
CM: [tex]\frac{AG}{MG} =2 = \frac{AH}{OM}[/tex] bằng tính chất đường trung bình trong [tex]\Delta[/tex]AHQ và tính chất trọng tâm trong [tex]\Delta[/tex]ABC
CM: [tex]\Delta[/tex]AHG và [tex]\Delta[/tex]MOG đồng dạng
\Rightarrow [tex]\widehat{AGH}=\widehat{MGO}[/tex] (1)
Ta có: [tex]\widehat{HGA} + \widehat{HGM} = 180^0 [/tex](2 góc kề bù) (2)
Từ (1) & (2) ta có: [tex]\widehat{MGO} + \widehat{HGM} = 180^0 [/tex]
\Rightarrow H, G, O thẳng hàng.
2. Chứng minh đường tròn Euler
Gọi K là trung điểm của OH
Cách 1:
Gọi I là trung điểm của AH
Xét [tex]\Delta[/tex]AHO có:
[tex]\{ \begin IA=IH (gt) \\KH=KO (gt)[/tex]
\Rightarrow IK là đường trung bình của [tex]\Delta[/tex]AHO
\Rightarrow IK//AO; [tex]IK=\frac{1}{2}AO=\frac{R}{2}[/tex] (1)
Cm tương tự: KM là đường trung bình của [tex]\Delta[/tex]HOQ
\Rightarrow KM//OQ; [tex]KM=\frac{1}{2}OQ=\frac{R}{2}[/tex] (2)
Từ (1), (2)
\Rightarrow [tex]\{ \begin KI=KM=\frac{R}{2} \\I, K, M [/tex]thẳng hàng
Xét [tex]\Delta[/tex]IDM vuông tại D có DK là trung tuyến (KI=KM)
\Rightarrow[tex]KI=KM=DK=\frac{R}{2}[/tex]
\RightarrowI, D, M [tex]\in\[/tex] [tex](K;\frac{R}{2})[/tex]
Cm tương tự: 2 chân đường cao vẽ từ B và C, 2 chân đường trung tuyến vẽ từ B và C, 2 trung điểm HB và HC [tex]\ \in\ (K;\frac{R}{2})[/tex]
Cách 2: Cập nhật sớm ^^!
3. Chứng minh định lý Euler
Cập nhật sớm ^^!
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
