E
everlastingtb91
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Câu I:
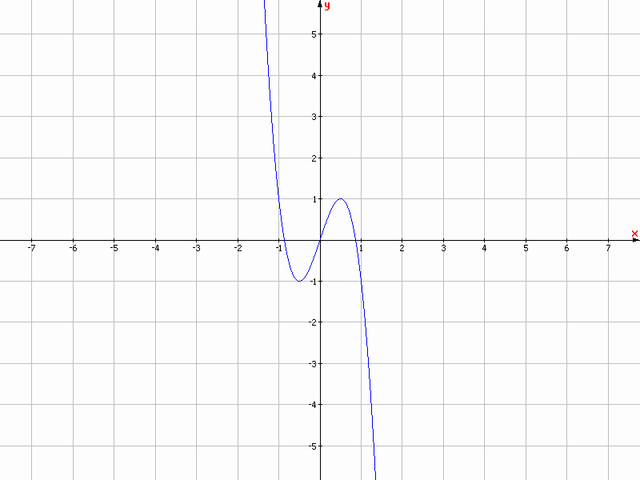
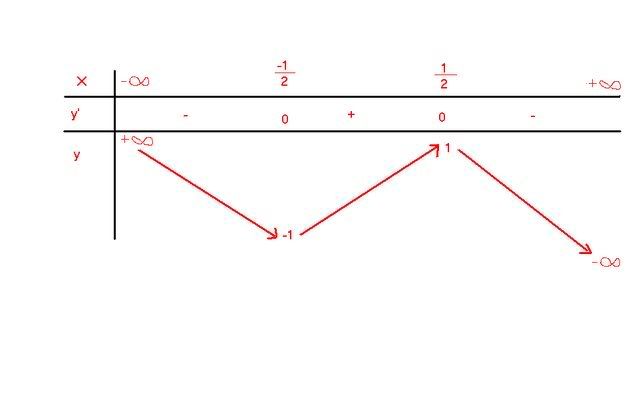
1, Khảo sát sự biến thiên và vẽ đồ thị hàm số [TEX]y=3x-4x^3 (C)[/TEX]
2, Tìm m để pt [TEX]3x-4x^3-3m+4m^3=0[/TEX] có 3 nghiệm phân biệt.
3,Viết phương trình tiếp tuyến với đồ thị (C) biết tiếp tuyến đi qua M (1;3)
Câu II: Giải phương trình:
[TEX]1,\log_3(\frac{3}{x}) (\log_2x)- log_3(\frac{x^3}{\sqrt{3}})=\frac{5}{3} log_2\sqrt{x}[/TEX]
[TEX]2, \frac{sin^4x+cos^4x}{5sin2x}=\frac{1}{2}cot2x -\frac{1}{8sin2x}[/TEX]
Câu III:
1, Tìm
[TEX]\lim_{x \to 2}\(\frac{\sqrt{x+2}-\sqrt[3]{x+6}}{2009(x-2)} )[/TEX]
2,Tính thể tích của hình SABC biết rằng đáy ABC là một tam giác đều có cạnh bằng a mặt bên (SAB) vuông góc với mặt đáy, hai mặt bên còn lại cùng tạo với mặt đáy một góc bằng [TEX]\alpha[/TEX] .
Câu IV:
1, Giải hệ phương trình:
[TEX]\left{2A_x^y+5C_x^y=90\\{5A_x^y -2C_x^y=80[/TEX]
2,Cho [TEX]x^2 +2y^2=3.[/TEX] Tìm gía trị lớn nhất của hàm số [TEX]f(x,y)=\mid x\mid +\sqrt{y^2+1}[/TEX]
Câu V:
1.Dành cho ban cơ bản:
Trong mặt phằng Oxy, cho hình thoi ABCD có A(0;2) B(4;5) và giao điểm của hai đường chéo nằm trên đường thẳng (d) có phương trình [TEX]x-y-1=0.[/TEX] Tính toạ độ các đỉnh C, D.
2. Dành cho ban tự nhiên:
Trong mặt phẳng Oxy cho đường thẳng [TEX]x-y+1=0 (d)[/TEX] và đường tròn [TEX]x^2+y^2+2x-4y=0 (C)[/TEX]
Tìm toạ độ điểm M thuộc đường thẳng (d) mà qua đó ta kẻ được hai đường thẳng tiếp xúc với đường trong (C) tại A và B sao cho góc AMB bằng 60* ( độ)
_____________________________________________________________The__________End____________________________________________________________________________________________________________________________________________________________
Các bạn thử giải cho mình đọ đáp án nhé! Vừa thi hôm 11/01/2009.
Cảm ơn!
1, Khảo sát sự biến thiên và vẽ đồ thị hàm số [TEX]y=3x-4x^3 (C)[/TEX]
2, Tìm m để pt [TEX]3x-4x^3-3m+4m^3=0[/TEX] có 3 nghiệm phân biệt.
3,Viết phương trình tiếp tuyến với đồ thị (C) biết tiếp tuyến đi qua M (1;3)
Câu II: Giải phương trình:
[TEX]1,\log_3(\frac{3}{x}) (\log_2x)- log_3(\frac{x^3}{\sqrt{3}})=\frac{5}{3} log_2\sqrt{x}[/TEX]
[TEX]2, \frac{sin^4x+cos^4x}{5sin2x}=\frac{1}{2}cot2x -\frac{1}{8sin2x}[/TEX]
Câu III:
1, Tìm
[TEX]\lim_{x \to 2}\(\frac{\sqrt{x+2}-\sqrt[3]{x+6}}{2009(x-2)} )[/TEX]
2,Tính thể tích của hình SABC biết rằng đáy ABC là một tam giác đều có cạnh bằng a mặt bên (SAB) vuông góc với mặt đáy, hai mặt bên còn lại cùng tạo với mặt đáy một góc bằng [TEX]\alpha[/TEX] .
Câu IV:
1, Giải hệ phương trình:
[TEX]\left{2A_x^y+5C_x^y=90\\{5A_x^y -2C_x^y=80[/TEX]
2,Cho [TEX]x^2 +2y^2=3.[/TEX] Tìm gía trị lớn nhất của hàm số [TEX]f(x,y)=\mid x\mid +\sqrt{y^2+1}[/TEX]
Câu V:
1.Dành cho ban cơ bản:
Trong mặt phằng Oxy, cho hình thoi ABCD có A(0;2) B(4;5) và giao điểm của hai đường chéo nằm trên đường thẳng (d) có phương trình [TEX]x-y-1=0.[/TEX] Tính toạ độ các đỉnh C, D.
2. Dành cho ban tự nhiên:
Trong mặt phẳng Oxy cho đường thẳng [TEX]x-y+1=0 (d)[/TEX] và đường tròn [TEX]x^2+y^2+2x-4y=0 (C)[/TEX]
Tìm toạ độ điểm M thuộc đường thẳng (d) mà qua đó ta kẻ được hai đường thẳng tiếp xúc với đường trong (C) tại A và B sao cho góc AMB bằng 60* ( độ)
_____________________________________________________________The__________End____________________________________________________________________________________________________________________________________________________________
Các bạn thử giải cho mình đọ đáp án nhé! Vừa thi hôm 11/01/2009.
Cảm ơn!
Last edited by a moderator: