B
binhtt
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Bài toán:
Xét
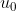là một số thực tùy ý và dãy số
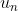được xác định bởi công thức:
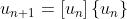(trong đó
là phần nguyên và phần lẻ của số thực
).
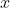Chứng minh rằng: tồn tại chỉ số
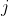sao cho
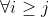, ta có
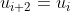
Lời giải:
- Với
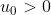, bài toán dễ dàng được giải quyết vì
)
. Áp dụng (*) một số lần đủ lớn, suy ra tồn tại 1 chỉ số
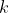sao cho
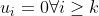
- Với
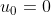hoặc
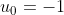, bài toán hiển nhiên đúng
- Với
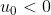, ta sẽ sử dụng 1 bổ đề như sau:
Cho
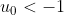và dãy
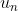được xác định theo công thức truy hồi nói trên. Chứng minh rằng: tồn tại chỉ số
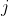sao cho,
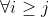, hoặc là
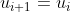, hoặc là
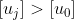
Do
)
nên rõ ràng ta chỉ cần tìm chỉ số
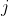sao cho
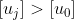
Giả sử chỉ số
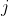không tồn tại, tức với mọi
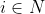ta có
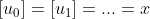. Khi đó
 - u_n = (x - 1)u_n - x^2)
và
u_{n + 1} - x^2 = (x - 1)(xu_n - x^2) - x^2 = x((x - 1)u_n - x^2) = x\delta (**))
Do
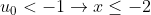nên từ (**) sẽ xảy ra 2 trường hợp:
+ Hoặc
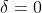, khi đó
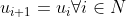. Bài toán được giải quyết
+ Hoặc
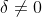, khi đó tồn tại số n đủ lớn sao cho
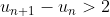. Hiển nhiên
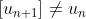, nhưng do (1) nên
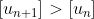
Bổ đề được giải quyết. Áp dụng bổ đề một số lần hữu hạn, ta quy bài toán về trường hợp
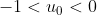. Nhưng trường hợp này là hiển nhiên vì
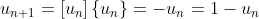
 = u_n)
Mình thấy bài toán này rất hay, các bạn xem xong chắc sẽ có thêm chút kinh nghiệm. :-SS
Xét
Chứng minh rằng: tồn tại chỉ số
Lời giải:
- Với
- Với
- Với
Cho
Do
Giả sử chỉ số
và
Do
+ Hoặc
+ Hoặc
Bổ đề được giải quyết. Áp dụng bổ đề một số lần hữu hạn, ta quy bài toán về trường hợp
Mình thấy bài toán này rất hay, các bạn xem xong chắc sẽ có thêm chút kinh nghiệm. :-SS