T
transformers123
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Bài 1: Chứng minh
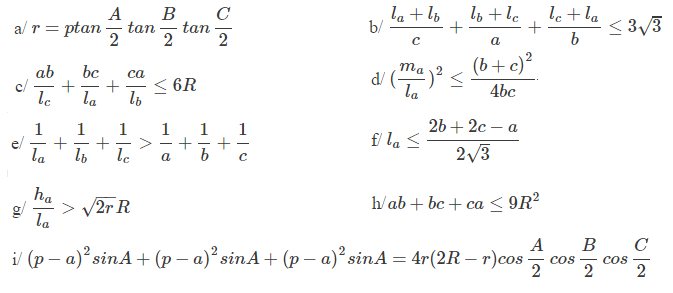
Bài 2:
Cho $\Delta ABC$ không tù, $I$ là trung điểm $BC$. Gọi $P,\ P_1,\ P_2$ lần lượt là chu vi tam giác $ABC,\ ABI,\ ACI$. Chứng minh $\Delta ABC$ vuông cân nếu $P^2=P_1^2+P_2^2$
Bài 3:
Cho tam giác $ABC$ nội tiếp đường tròn $(O)$. Đường phân giác trong góc $A$ cắt $BC$ tại $A_1$, cắt $(O)$ tại $A_2$. Các điểm $B_1,\ B_2,\ C_1,\ C_2$ xác định tương tự
a/ Chứng minh $\dfrac{AA_1}{AA_2}+\dfrac{BB_1}{BB_2}+\dfrac{CC_1}{CC_2} \le \dfrac{9}{4}$
b/ Chứng minh bất đẳng thức trên vẫn đúng khi thay giả thiết ba đường phân giác thành ba đường trung tuyến tương ứng
c/ Chứng minh bất đẳng thức trên đổi chiều khi thay giả thuyết ba đường phân giác thành ba đường cao tương ứng
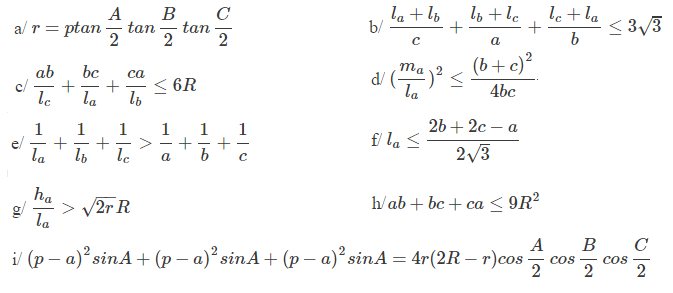
Bài 2:
Cho $\Delta ABC$ không tù, $I$ là trung điểm $BC$. Gọi $P,\ P_1,\ P_2$ lần lượt là chu vi tam giác $ABC,\ ABI,\ ACI$. Chứng minh $\Delta ABC$ vuông cân nếu $P^2=P_1^2+P_2^2$
Bài 3:
Cho tam giác $ABC$ nội tiếp đường tròn $(O)$. Đường phân giác trong góc $A$ cắt $BC$ tại $A_1$, cắt $(O)$ tại $A_2$. Các điểm $B_1,\ B_2,\ C_1,\ C_2$ xác định tương tự
a/ Chứng minh $\dfrac{AA_1}{AA_2}+\dfrac{BB_1}{BB_2}+\dfrac{CC_1}{CC_2} \le \dfrac{9}{4}$
b/ Chứng minh bất đẳng thức trên vẫn đúng khi thay giả thiết ba đường phân giác thành ba đường trung tuyến tương ứng
c/ Chứng minh bất đẳng thức trên đổi chiều khi thay giả thuyết ba đường phân giác thành ba đường cao tương ứng
Last edited by a moderator:

