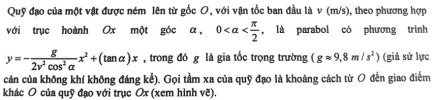[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Quỹ đạo của một vật được ném lên từ gốc [imath]O[/imath] với vận tốc ban đầu [imath]v(m/s)[/imath], theo phương hợp với [imath]Ox[/imath] một góc [imath]0<\alpha<\dfrac{\pi}{2}[/imath], là parabol có phương trình [imath]y=-\dfrac{g}{2v^2\cos^2\alpha}x^2+(\tan \alpha)x[/imath]. Gọi tầm xa quỹ đạo [imath]x[/imath] là khoảng cách từ [imath]O[/imath] tới giao điểm khác [imath]O[/imath] của quỹ đạo với trục [imath]Ox[/imath]. Khi [imath]\alpha[/imath] thay đổi, tìm [imath]\alpha[/imath] sao cho [imath]x[/imath] đạt giá trị lớn nhất và tính [imath]x_{\max}[/imath] tại giá trị [imath]\alpha[/imath] đó.
Mình cảm ơn các bạn nhiều ạ.
@Mộc Nhãn @Cáp Ngọc Bảo Phương @kido2006 @vangiang124
Mình cảm ơn các bạn nhiều ạ.
@Mộc Nhãn @Cáp Ngọc Bảo Phương @kido2006 @vangiang124
Attachments
Last edited by a moderator: