View attachment 220767
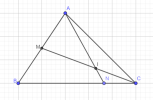
[imath]\overrightarrow{AN}=\overrightarrow{AB}+\overrightarrow{BN}[/imath]
[imath]=\overrightarrow{AB}+\dfrac{4}5\overrightarrow{BC}=\overrightarrow{AB}+\dfrac{4}5(\overrightarrow{AC}-\overrightarrow{AB})[/imath]
[imath]=\dfrac{1}5\overrightarrow{AB}+\dfrac{4}5\overrightarrow{AC}[/imath]
Đặt [imath]\overrightarrow{AI}=k\overrightarrow{AN}[/imath]
[imath]\overrightarrow{MC}=\overrightarrow{AC}-\overrightarrow{AM}=-\dfrac{1}2\overrightarrow{AB}+\overrightarrow{AC}[/imath]
[imath]\overrightarrow{MI}=\overrightarrow{AI}-\overrightarrow{AM}=k(\dfrac{1}5\overrightarrow{AB}+\dfrac{4}5\overrightarrow{AC})-\dfrac{1}2\overrightarrow{AB}[/imath]
[imath]=(\dfrac{k}5-\dfrac{1}2)\overrightarrow{AB}+\dfrac{4k}5\overrightarrow{AC}[/imath]
Mà [imath]M,I,C[/imath] thẳng hàng nên [imath]\overrightarrow{MI}=\overrightarrow{MC}[/imath]
[imath]\iff (\dfrac{k}5-\dfrac{1}2)\overrightarrow{AB}+\dfrac{4k}5\overrightarrow{AC}=\dfrac{-l}2\overrightarrow{AB}+l\overrightarrow{AC}[/imath]
[imath]\iff \left\{\begin{matrix}\dfrac{k}5-\dfrac{1}2=\dfrac{-l}2\\\dfrac{4k}5=l\end{matrix}\right.\iff k=\dfrac{5}6, l=\dfrac{2}3[/imath]
Vậy [imath]\overrightarrow{AI}=\dfrac{5}6\overrightarrow{AN}[/imath]
Có gì khúc mắc em hỏi lại nha
Ngoài ra, em xem thêm tại
Tổng hợp sách giáo khoa mới toán 10
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.