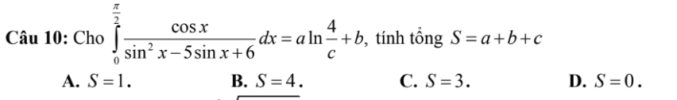[imath]\displaystyle \int^{\pi / 2}_{0}{ \dfrac{ \cos{x}}{\sin^2{x}-5 \sin{x}+6}} \mathrm{d} x[/imath]
Đặt [imath]t = \sin{x} \ (t \in [-1;1]) \Rightarrow \mathrm{d} t = \cos{x} \mathrm{d} x [/imath]
Đổi cận:
[imath]x=0 \Rightarrow t=0 \\
x= \dfrac{ \pi}{2} \Rightarrow t=1[/imath]
Ta có: [imath]\displaystyle \int^{1}_{0}{ \dfrac{ \mathrm{d}t}{t^2-5t+6}}[/imath]
[imath]\dfrac{1}{t^2-5t+6} = \dfrac{1}{(t-2)(t-3)} \\
= \dfrac{A}{t-2} + \dfrac{B}{t-3} \\
= \dfrac{A(t-3) + B(t-2)}{(t-2)(t-3)} \\
= \dfrac{(A+B)t-3A-2B}{(t-2)(t-3)}[/imath]
Ta có hệ: [imath]
\left\{\begin{matrix}
A+B=0 \\
-3A-2B=1
\end{matrix}\right. \\
\Leftrightarrow \left\{\begin{matrix}
A=-1 \\
B=1
\end{matrix}\right.
[/imath]
Nên ta có: [imath]\displaystyle \int^{1}_{0}{ \dfrac{ \mathrm{d}t}{t^2-5t+6}} = \displaystyle \int^{1}_{0}{ \left ( \dfrac{ -1}{t-2} + \dfrac{1}{t-3} \right )} \mathrm{d}t \\
=- \int^{1}_{0}{ \dfrac{ 1}{t-2} } \mathrm{d}t + \int^{1}_{0}{\dfrac{1}{t-3} } \mathrm{d}t \\
=- ( \ln|t-2|)|^1_0 + ( \ln|t-3|)|^1_0 \\
= -( \ln{1} - \ln{2} )+ ( \ln{2} - \ln{3}) \\
= 2 \ln{2} - \ln{3} \\
= \ln{2^2} - \ln{3} \\
= \ln{ \left ( \dfrac{4}{3} \right )}[/imath]
[imath]\displaystyle \int^{\pi / 2}_{0}{ \dfrac{ \cos{x}}{\sin^2{x}-5 \sin{x}+6}} \mathrm{d} x = a \ln { \left ( \dfrac{4}{c} \right )} +b[/imath]
Suy ra [imath]a=1, \ b=0, \ c=3[/imath]
[imath]S=a+b+c=4[/imath]
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.