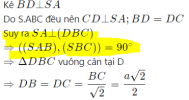Cho khối chóp đều S.ABC có cạnh đáy bằng a. Hai mặt phẳng (SAB) và (SBC) vuông góc với nhau. Thể tích khối chóp đã cho bằng?
huyenhuyen146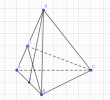
Kẻ [imath]BD\bot SA[/imath]
Do S.ABC đều nên [imath]CD\bot SA; BD=DC[/imath]
Suy ra [imath]SA\bot(DBC)[/imath]
[imath]\Rightarrow ((SAB),(SBC))=90^\circ[/imath]
[imath]\Rightarrow \Delta DBC[/imath] vuông cân tại D
[imath]\Rightarrow DB=DC=\dfrac{BC}{\sqrt2}=\dfrac{a\sqrt2}{2}[/imath]
Đặt [imath]SA=SB=SC=b[/imath]
Kẻ [imath]SI\bot AB[/imath]
[imath]\Rightarrow SI=\sqrt{b^2-\dfrac{a^2}{4}}[/imath]
Ta có: [imath]2S_{SAB}=SI.AB=BD.AS[/imath]
[imath]\Rightarrow a\sqrt{b^2-\dfrac{a^2}{4}}=\dfrac{ab\sqrt2}{2}\Rightarrow b=\dfrac{a\sqrt2}{2}[/imath]
Đến đây chắc em dễ dàng tìm được V rồi nhỉ
Có gì khúc mắc em hỏi lại nhé
Ngoài ra em tham khảo thêm tại
Chinh phục kì thi THPTQG môn Toán 2022
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
