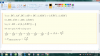
Cho hình lăng trụ tứ giác đều ABCD.A'B'C'D' cạnh đáy bằng a, khoảng cách từ A đến (A'BC) bằng a/3, tính thể tích lăng trụ. Em cám ơn ạ!
Ta có:
[tex]BC \bot AA',BC \bot AB \Rightarrow BC \bot \left( {ABA'} \right) \Rightarrow \left( {A'BC} \right) \bot \left( {ABA'} \right)[/tex]
Kẻ [tex]AH \bot A'B \Rightarrow AH \bot \left( {A'BC} \right)[/tex]
↔ [tex]AH = d\left( {A,\left( {A'BC} \right)} \right) = \frac{a}{3}[/tex]
Xét tam giác A’AB vuông tại A:
[tex]\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A'{A^2}}} \Rightarrow \frac{1}{{A'{A^2}}} = \frac{1}{{A{H^2}}} - \frac{1}{{A{B^2}}} = \frac{8}{{{a^2}}} \Rightarrow A'A = \frac{{a\sqrt 2 }}{4}[/tex]
↔[tex]\Rightarrow {V_{ABCD.A'B'C'D'}} = \frac{{{a^3}\sqrt 2 }}{4}[/tex]
→Đpcm
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
